GetStudySolution

Getstudysolution is an online educational platform that allows students to access quality educational services and study materials at no cost.

NCERT Solutions for class 10 Maths chapter 10 – Circles

Back Exercise

Exercise 10.1

Question 1.
How many tangents can a circle have?
Solution:
Infinitely many tangents.

Question 2.
Fill in the blanks:
(i) A tangent to a circle intersects it in ………… point(s).
(ii) A line intersecting a circle in two points is called a………….
(iii) A circle can have ………………. parallel tangents at the most.
(iv) The common point of a tangent to a circle and the circle is called…………
Solution:
(i) One
(ii) Secant
(iii) Two
(iv) Point of contact.

Question 3.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is
(a) 12 cm
(b) 13 cm
(c) 8.5 cm
(d) cm
Solution:
Given: OQ = 12 cm and OP = 5 cm

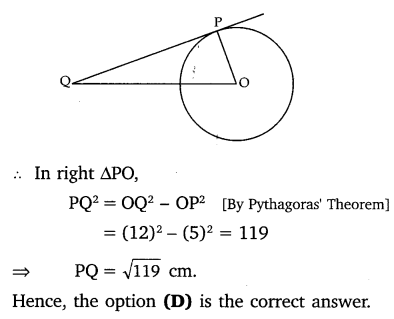
Question 4.
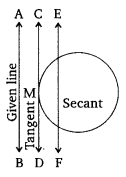
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Solution:
Here, AB is the given line. CD is tangent to the given circle at the point M and parallel to AB, and EF is a secant parallel to AB.

Exercise 10.2

Question 1.
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the center is 25 cm. The radius of the circle is
(a) 7 cm
(b) 12 cm
(c) 15 cm
(d) 24.5 cm
Solution:
The correct option is (A).

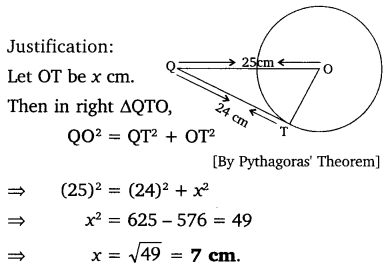
Question 2.
In the figure, if TP and TQ are the two tangents to a circle with center O so that ∠POQ = 110°, then ∠PTQ is equal to
(a) 60°
(b) 70°
(c) 80°
(d) 90°

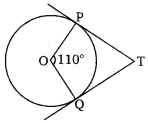
Solution:
The correct option is (B).

Question 3.
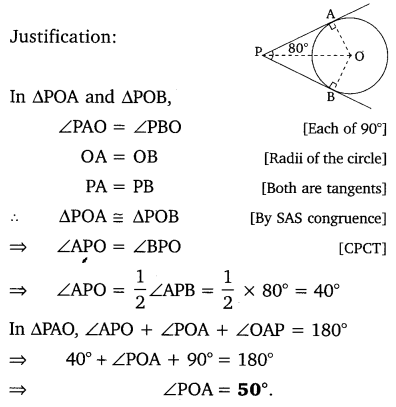
If tangents PA and PB from a point P to a circle with center O are inclined to each other at angle of 80°, then ∠POA is equal to
(a) 50°
(b) 60°
(c) 70°
(d) 80°
Solution:
The correct option is (A).

Question 4.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Solution:

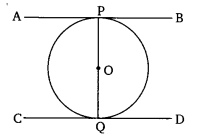
Let PQ be the diameter of a circle with center O. AB and CD are two tangents drawn to the circle at P and Q respectively.
We have, OP ⊥ AB and OQ ⊥ CD    [By theorem]
∠BPO = ∠CQO = 90°          [Each of 90°]
⇒ AB ∥ CD [ Transversal PQ makes equal interior alternate angles]

Question 5.
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the center.
Solution:

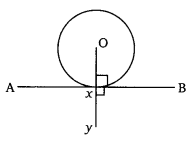
In the given figure, AXB is the tangent to a circle with center O.
Here, OX is the line perpendicular to the tangent AXB at the point of contract X.
The, we have:
∠OXB + ∠BXY = 90° + 90° = 180°
⇒ OXY is collinear, i.e., OX passes through the center of the circle.
Hence, Proved.

Question 6.
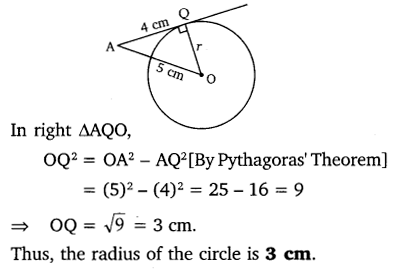
The length of a tangent from a point A at distance 5 cm from the center of the circle is 4 cm. Find the radius of the circle.
Solution:
In the figure, AQ = 4 cm and AO = 5 cm.

Question 7.
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Solution:
In the given figure, PQ is the chord of the larger circle, which touches the smaller circle at R.

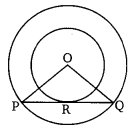
Question 8.
A quadrilateral ABCD is drawn to circumscribe a circle (see figure). Prove that AB + CD = AD + BC.

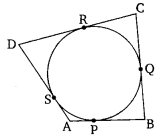
Solution:

Question 9.
In the figure, XY and X’Y’ are two parallel tangents to a circle, x with center O and another tangent AB with a point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°.

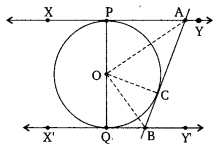
Solution:

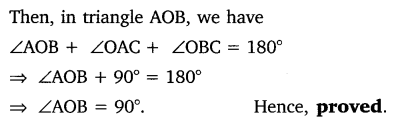
Question 10.
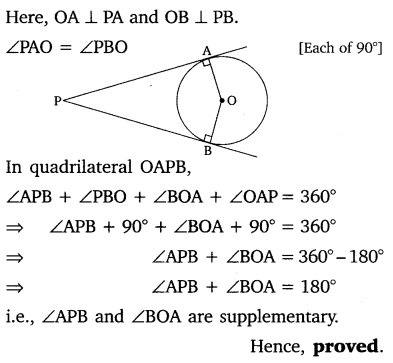
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the center.
Solution:
From the figure, PA and PB are tangents drawn from an external point P to the circle with center O. A and B are the points of contact of the tangents.

Question 11.
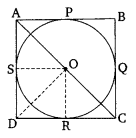
Prove that the parallelogram circumscribing a circle is a rhombus.
Solution:
We have a parallelogram ABCD which circumscribes a circle with center O. P, Q, R and S are the points of contact of sides AB, BC, CD, and DA respectively.

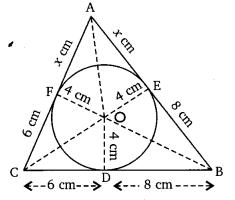
Question 12.
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see figure). Find the sides AB and AC.

Solution:

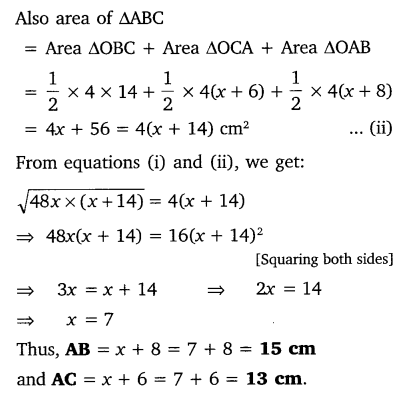
Question 13.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the center of the circle.
Solution:
In the figure, P, Q, R, and S are the points touching the circle and sides AB, BC, CD, and DA of the quadrilateral ABCD respectively.

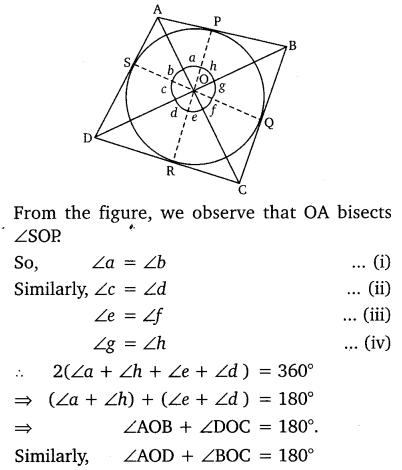
Thus, opposite sides of quadrilateral ABCD subtend supplementary angles at the center of a circle.
Hence, Proved.