GetStudySolution

Getstudysolution is an online educational platform that allows students to access quality educational services and study materials at no cost.

NCERT Solutions for class 9 Maths chapter 11 – Constructions

Back Exercise

Exercise 11.1

Question 1.
Construct an angle of 90° at the initial point of a given ray and justify the construction.
Solution:
Steps of construction

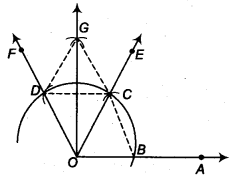
1. Taking O as centre and some radius, draw an arc of a circle which intersects OA say at a point B.
2. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
3. Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.
4. Draw the ray OE passing through C.
   Then, ∠EOA = 60°
5. Draw the ray of passing through D. Then, ∠FOE = 60°.
6. Next, taking Cand Das centres and with the radius more than $\frac { 1 }{ 2 }$ CD, draw arcs to intersect each other, say at G.
7. Draw the ray OG. This ray OG is the bisector of the ∠FOE i.e.,
   ∠FOG = ∠EOG = $\frac { 1 }{ 2 }$ ∠FOE = $\frac { 1 }{ 2 }$ (60°) = 30°
   Thus, ∠GOA = ∠GOE + ∠EOA
   = 30° + 60° = 90°

Justification
(i) Join BC.
Then, OC=OB = BC (By construction)
∴ ∆COB is an equilateral triangle.
∴ ∠COB = 60°
∴ ∠EOA = 60°

(ii) Join CD.
Then, OD=OC=CD (By construction)
∴ ∆DOC is an equilateral triangle.
∴ ∠DOC = 60°
∴ ∠FOE = 60°

(iii) Join CG and DG.
In ∆ODG and ∆OCG,
OD = OC (Radii of the same arc)
DG = CG (Arcs of equal radii)
OG = OG (Common)
∴ ∆ ODG ≅ ∆OCG (SSS rule)
∴ ∠DOG = ∠COG (CPCT)
∴ ∠FOG = ∠EOG = $\frac { 1 }{ 2 }$ ∠FOE
= $\frac { 1 }{ 2 }$ (60°) = 30°
Thus, ∠GOA = ∠GOE + ∠EOA = 30° + 60° = 90°

Question 2.
Construct an angle of 45° at the initial point of a given ray and justify the construction.
Solution:
Steps of construction

1. Taking O as centre and some radius, draw an arc of a circle which intersects OA, say at a point B.
2. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
   
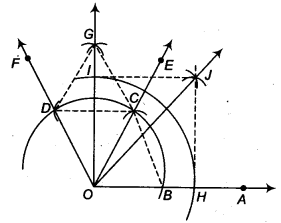
3. Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.
4. Draw the ray OE passing through C. Then, ∠EOA = 60°.
5. Draw the ray OF passing through D. Then, ∠FOE = 60°.
6. Next, taking C and D as centres and with radius more than $\frac { 1 }{ 2 }$ CD, draw arcs to intersect each other, say at G.
7. Draw the ray OG. This ray OG is the bisector of the ∠FOE,
   i.e., ∠FOG = ∠EOG = $\frac { 1 }{ 2 }$ ∠FOE = $\frac { 1 }{ 2 }$ (60°) = 30°.
   thus , ∠GOA = ∠GOE + ∠EOA
   = 30° + 60° = 90°
8. Now taking O as centre and any radius, draw an arc to intersect the rays OA and OG, say at Hand /, respectively.
9. Next, taking H and las centres and with the radius more than $\frac { 1 }{ 2 }$ Hl, draw
   arcs to intersect each other, say at J.
10. Draw the ray OJ. This ray OJ is the required bisector of the ∠GOA.
    ∠GOJ = ∠AOJ = $\frac { 1 }{ 2 }$ ∠GOA
    = $\frac { 1 }{ 2 }$ (90°) = 45°

Justification
(i) Join BC. (By construction)
Then, OC = OB = BC
∴ ∆COB is an equilateral triangle.
∴ ∠COB = 60°
∴ ∠EOA = 60°

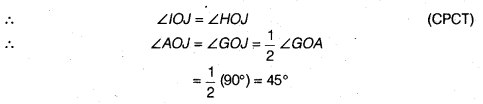
Question 3.
Construct the angles of the following measurements
(i) 30°
(ii) 22 $\frac { 1 }{ 2 }$ °
(iii) 15°
Solution:
(i) Steps of construction

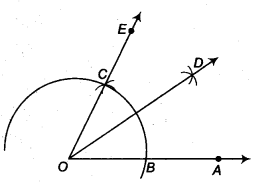
1. Taking O as centre and some radius, draw an arc of a circle which intersects OA, say at a point B.
2. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
3. Draw the ray OE passing through C. Then, ∠EOA = 60°.
4. Taking B and C as centres and with the radius more than $\frac { 1 }{ 2 }$ BC, draw arcs to intersect each other, say at D.
5. Draw the ray OD, this ray OD is the bisector of the ∠EOA, i.e.,
   ∠EOD = ∠AOD = $\frac { 1 }{ 2 }$ ∠EOA = $\frac { 1 }{ 2 }$ (60°) = 30°

(ii) Steps of construction

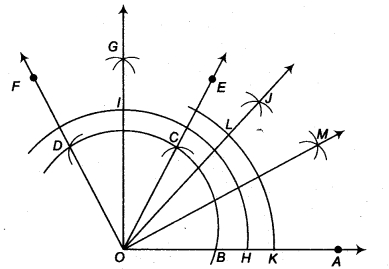
1. Taking O as centre and some radius, draw an arc of a circle which, intersects OA, say at a point B.
2. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
3. Taking C as centre and with the same radius as before, drawn an arc intersecting the arc drawn in step 1, say at D.
4. Draw the ray OE passing through C. Then, ∠EOA = 60°.
5. Draw the ray OF passing through D. Then, ∠FOE = 60°.
6. Next, taking C and D as centres and with radius more than $\frac { 1 }{ 2 }$CD, draw arcs to intersect each other, say at G.
7. Draw the ray OG. This ray OG is the bisector of the ∠FOE,
   
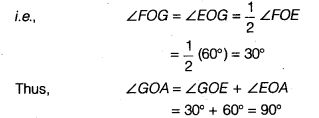
8. Now, taking O as centre and any radius, draw an arc to intersect the rays OA and OG, say at H and l, respectively.
9. Next, taking H and l as centres and with the radius more than $\frac { 1 }{ 2 }$Hl, draw arcs to intersect each other, say at J.
10. Draw the ray OJ. This ray OJ is the bisector of the ∠GOA
    i. e., ∠GOJ = ∠AOJ = $\frac { 1 }{ 2 }$ ∠GOA
    = $\frac { 1 }{ 2 }$ (90°) = 45 °
11. Now, taking O as centre and any radius, drawn an arc to intersect the rays OA and OJ, say at K and L, respectively.
12. Next, taking K and L as centres and with the radius more than $\frac { 1 }{ 2 }$KL, draw arcs to intersect each other, say at H.
13. Draw the ray OM. This ray OM is the bisector of the ∠AOJ, i.e., ∠JOM = ∠AOM
    = $\frac { 1 }{ 2 }$ ∠AOJ = $\frac { 1 }{ 2 }$ (45°) = 22 $\frac { 1 }{ 2 }$ °

(iii) Steps of construction

1. Taking O as centre and some radius, draw an arc of a circle which intersects OA say at a point B.
2. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C..
3. Draw the ray OE passing through C. Then, ∠EOA = 60°.
   
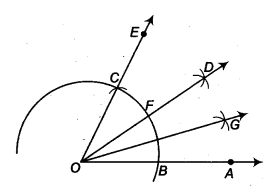
4. Now, taking 6 and Cas centres and with the radius more than $\frac { 1 }{ 2 }$ BC, draw arcs to intersect each other, say at D.
5. Draw the ray OD intersecting the arc drawn in step 1 at F. This ray OD is the bisector of the ∠EOA, i.e.,
   ∠EOD = ∠AOD = $\frac { 1 }{ 2 }$ ∠EOA = $\frac { 1 }{ 2 }$ (60°) = 30°
6. Now, taking B and F as centres and with the radius more than $\frac { 1 }{ 2 }$ BF, draw arcs to intersect each other, say at G.
   1. Draw the ray OG. This ray OG is the bisector of the ∠AOD,
      i. e., ∠DOG = ∠AOG = $\frac { 1 }{ 2 }$ ∠AOD = $\frac { 1 }{ 2 }$ (30°) = 15°

Question 4.
Construct the following angles and verify by measuring them by a protractor
(i) 75°
(ii) 105°
(iii) 135°
Solution:
(i) Steps of construction

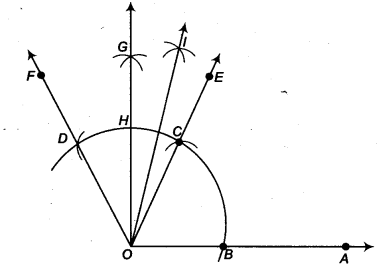
1. Taking O as centre and some radius, draw an arc of a circle which intersects OA say at a point B.
2. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
3. Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.
4. Join the ray OE passing through C. Then, ∠EOA = 60°.
5. Draw the ray of passing through D. Then, ∠FOE = 60°.
6. Next, taking C and D as centres and with the radius more than $\frac { 1 }{ 2 }$CD, draw arcs to intersect each other, say at G.
7. Draw the ray OG intersecting the arc of step 1 at H. This ray OG is the bisector of the ∠FOE, i.e., ∠FOG = ∠EOG
   = $\frac { 1 }{ 2 }$ ∠FOE = $\frac { 1 }{ 2 }$(60°) = 30°
8. Next, taking Cand H as centres and with the radius more than $\frac { 1 }{ 2 }$CH, draw
   arcs to intersect each other, say at l.
   Draw the ray OI. This ray OI is the bisector of the ∠GOE,
   i. e., ∠GOI = ∠EOI = $\frac { 1 }{ 2 }$ ∠GOE = $\frac { 1 }{ 2 }$ (30°) = 15°
   Thus, ∠IOA = ∠IOE + ∠EOA
   =15°+ 60° = 75°
   On measuring the ∠IOA by protractor, we find that ∠IOA = 15°
   Thus, the construction is verified.

(ii) Steps of construction

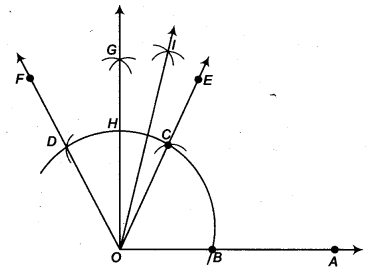
1. Taking O as centre and some radius, draw an arc of a circle which intersects OA say at a point B.
2. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
3. Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at a point D.
4. Draw the ray Of passing through C. Then, ∠EOA = 60°.
5. Draw the ray OF passing through D. Then, ∠FOE = 60°.
6. Next, taking Cand Das centres and with the radius more than $\frac { 1 }{ 2 }$ CD, draw arcs to intersect each other, say at G.
7. Draw the ray OG intersecting the arc drawn in step 1 at H. This ray OG is the bisector of the ∠FOE, i.e.,
   
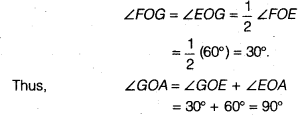
8. Next, taking H and D as centres and with the radius more than $\frac { 1 }{ 2 }$ HD, draw arcs to intersect each other, say at l.
9. Draw the ray Ol. This ray Ol is the bisector of the ∠FOG, i.e.,
   
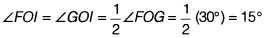
   Thus, ∠lOA = ∠IOG + ∠GOA = 15° + 90° = 105°. On measuring the ∠lOA by protractor, we find that ∠FOA = 105°.
   Thus, the construction is verified.
   
   

(iii) Steps of construction

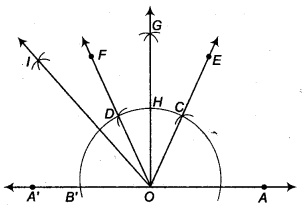
1. Produce AO to A’ to form ray OA’.
2. Taking O as centre and some radius, draw an arc of a circle which intersects OA at a point B and OA’ at a point B’.
3. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at a point C.
4. Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.
5. Draw the ray OE passing through C, then ∠EOA = 60°.
6. Draw the ray OF passing through D, then ∠FOE = 60°.
7. Next, taking C and D as centres and with the radius more than $\frac { 1 }{ 2 }$ CD, draw arcs to intersect each other, say at G.
8. Draw the ray OGintersecting the arc drawn in step 1 at H. This ray OG is the bisector of the ∠FOE i,e.,
   
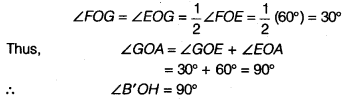
9. Next, taking B’ and H as centres and with the radius more than $\frac { 1 }{ 2 }$ B’H, drawn arcs to intersect each other, say at l.
10. Draw the ray Ol. This ray Ol is the bisector of the ∠B’OG i.e.,
    
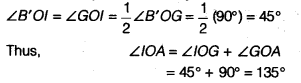
    On measuring the ∠IOA by protractor, we find that ∠lOA = 135°.
    Thus, the construction is verified.

Question 5.
Construct an equilateral triangle, given its side and justify the construction.
Solution:
Steps of construction

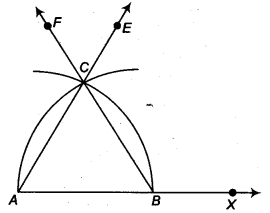
1. Take a ray AX with initial point A From AX, cut off AB = 4 cm.
2. Taking A as centre and radius (= 4 cm), draw an arc of a circle, which intersects AX, say at a point B.
3. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
4. Draw the ray AE passing through C.
5. Next, taking B as centre and radius (= 4 cm), draw an arc of a circle, which intersects AX, say at a point A
6. Taking A as centre and with the same radius as in step 5, draw an arc intersecting the previously drawn arc, say at a point C.
   Draw the ray BF passing through C.
   Then, ∆ ABC is the required triangle with gives side 4 cm.

Justification
AB = BC (By construction)
AB = AC (By construction)
∴ AB = BC = CA
∴ ∆ ABC is an equilateral triangle.
∴ The construction is justified.

Exercise 11.2

Question 1.
Construct a ∆ ABC in which BC = 7 cm, ∠B = 75° and AB + AC = 13 cm.
Solution:
Given that, in ∆ ABC, BC = 7 cm, ∠B = 75° and AS + AC = 13 cm
Steps of construction

1. Draw the base BC = 7 cm
   
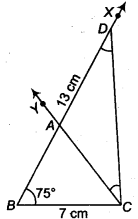
2. At the point 6 make an ∠XBC = 75°.
3. Cut a line segment BD equal to AB + AC = 13 cm from the ray BX.
4. Join DC.
5. Make an ∠DCY = ∠BDC.
6. Let CY intersect BX at A.
   Then, ABC is the required triangle.

Question 2.
Construct a ∆ ABC in which BC = 8 cm, ∠B = 45° and AB – AC = 35 cm.
Solution:
Given that, in ∆ ABC,
BC = 8 cm, ∠B = 45°and AB – AC = 3.5 cm

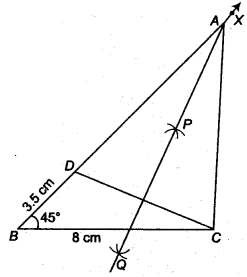
Steps of construction

1. Draw the base BC = 8 cm
2. At the point B make an ∠XBC = 45°.
3. Cut the line segment BD equal to AB – AC = 3.5 cm from the ray BX.
4. Join DC.
5. Draw the perpendicular bisector, say PQ of DC.
6. Let it intersect BX at a point A
7. Join AC.

Question 3.
Construct a ∆ ABC in which QR = 6 cm, ∠Q = 60° and PR – PQ = 2 cm.
Solution:
Given that, in ∆ ABC, QR = 6 crn ∠Q = 60° and PR – PQ = 2 cm
Steps of construction

1. Draw the base QR = 6 cm
2. At the point Q make an ∠XQR = 60°.
3. Cut line segment QS = PR- PQ (= 2 cm) from the line QX extended on opposite side of line segment QR.
4. Join SR.
5. Draw the perpendicular bisector LM of SR.
6. Let LM intersect QX at P.
7. Join PR.
   

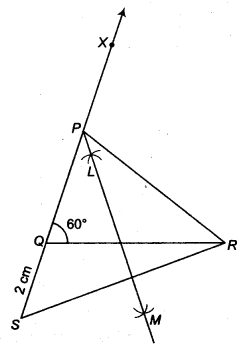
Question 4.
Construct a ∆ XYZ in which ∠Y = 30°, ∠Y = 90° and XY + YZ + ZX = 11 cm.
Solution:
Given that, in ∆XYZ ∠Y = 30°, ∠Z = 90° and XY + YZ + ZX = 11cm

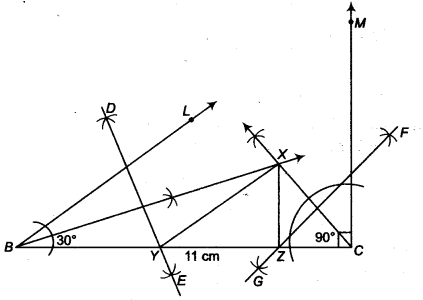
Steps of construction

1. Draw a line segment BC = XY + YZ + ZX = 11 cm
2. Make ∠LBC = ∠Y = 30° and ∠MCB = ∠Z = 90°.
3. Bisect ∠LBC and ∠MCB. Let these bisectors meet at a point X.
4. Draw perpendicular bisectors DE of XB and FG of XC.
5. Let DE intersect BC at Y and FC intersect BC at Z.
6. Join XY and XZ.
   Then, XYZ is the required triangle.

Question 5.
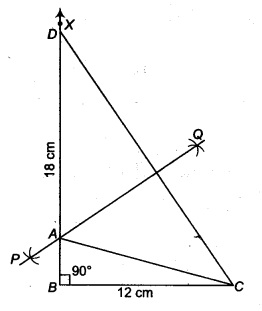
Construct a right triangle whose base is 12 cm and sum of its hypotenuse and other side is 18 cm.
Solution:
Given that, in A ABC, base BC = 12 cm, ∠B = 90° and AB + BC= 18 cm.
Steps of construction

1. Draw the base BC = 12 cm
2. At the point 6, make an ∠XBC = 90°.
3. Cut a line segment BD = AB+ AC = 18 cm from the ray BX.
4. Join DC.
5. Draw the perpendicular bisector PQ of CD to intersect SD at a point A

Join AC.
Then, ABC is the required right triangle.