GetStudySolution
Getstudysolution is an online educational platform that allows students to access quality educational services and study materials at no cost.
NCERT Solutions for class 10 Maths chapter 11 – Constructions
Back Exercise
Exercise 11.1
Question 1.
Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts.
Solution:
Steps of Construction:
1. Draw a line segment AB = 7.6 cm.
2. Draw another line segment (or ray) AX at any convenient acute angle with AB.
3. Along AX, locate 13 (5 + 8) points A1, A2, A3, …… , A13 such that AA1 = A1A2 = ……… = A12A13
4. Join BA13.
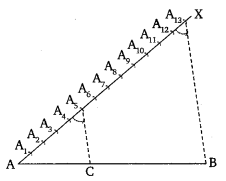
5. At point, A5 draw a straight line A5C parallel to A13B making an angle equal to ∠AA13B.
Thus, the point C divides the line segment AB in the ratio 5: 8.
Justification:

Question 2.
Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are of the corresponding sides of the first triangle.
Solution:
Steps of Construction:
1. Draw AC – 6 cm (ii) With A and Cas centers and radii 4 cm.
2. 5 cm respectively draw two ares intersecting each other at B. Join BA and BC.
3. Draw a ray AY making an acute angle with AC.
4. Locate three points and Ron AY, such that AP – POQR.
5. Join CR.
6. Through o. draw a line QC’ parallel to RC (by making an angle equal to ∠ARC) meeting the line segment AC at C’.
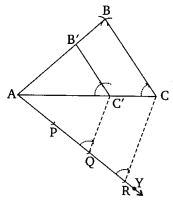
7. Similarly, through C, draw a line B’C parallel to CB
Thus, ABC is the required triangle, which is similar to ∆ABC with scale factor
Justification:
By construction, we have:

Question 3.
Construct a triangle with sides 5 cm, 6 cm, and 7 cm and then another triangle whose sides are of the corresponding sides of the first triangle.
Solution:
Steps of Construction:
1. Construct AABC such that AB = 5 cm, BC = 6 cm and CA = 7 cm.
2. Draw a ray BX making an acute angle with BC.
3. Locate 7 points on BX such that BD = DE = EF = FG – GH – IJ.
4. Join HC.
5. Through J, draw a line JC parallel to HC, meeting produced line BC at C’.
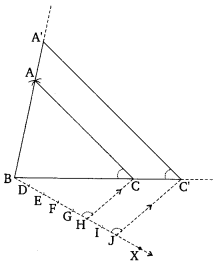
6. Through C’, draw a line 7 parallel to CA meeting the produced line BA at A’.
Thus A∆ABC is a required triangle
Justification:
By construction, we have:

Question 4.
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 1 times the corresponding sides of the isosceles triangle.
Solution:
Steps of Construction:
1. Construct an isosceles triangle ABC in which BC – 8 cm and altitude AD is 4 cm.
2. Draw a ray BX, making an acute angle with BC.
3. Locate 3 points on BX, such that BP – PQ = QR.
4. Join QC.
5. Through R, draw a line RC parallel to QC, meeting produced line BC at C’.
6. Through C, draw a line CA parallel to CA, meeting the produced line BA at A’.
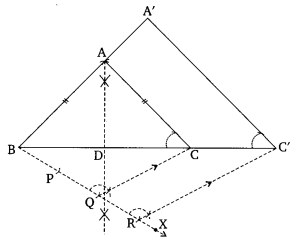
Thus, ∆A’BC’ is the required isosceles triangle
Justification:
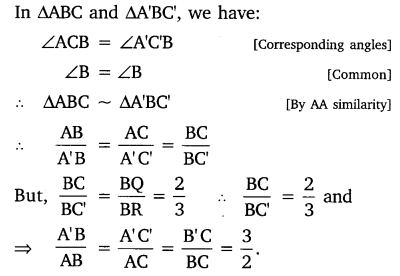
Question 5.
Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a triangle whose sides are of the corresponding sides of the triangle ABC.
Solution:
Steps of Construction:
1. Construct a ABC in which BC = 6 cm, AB = 5 cm and ∠ABC = 60°.
2. Draw a ray BX making any acute angle with BC.
3. Locate 4 points B1, B2, B3 and B4 on BX, such that BB1 = B1B2 = B2B3 =B3B4
4. Join B4C.
5. Through B3 draw a line B3C’ parallel to B4C, intersecting the line segment BC at C’.
6. Through C, draw a line parallel to CA, intersecting the line segment BA at A’.

Thus, ∆A’BC’ is the required triangle.
Justification:

Question 6.
Draw a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then, construct a triangle whose sides are times the corresponding sides of ∆ABC.
Solution:
Steps of Construction:
1. Draw a line segment BC – 7 cm.
2. Draw ∠ABC = 45° and ∠ACB = 30°, i.e., ∠BAC = 105°.
3. We get ∆ABC
4. Draw a ray BX making an acute angle with BC
5. Mark four points B1, B2, B3 and B4 on BX, such that BB1 = B1B2 = B2B3 = B3B4.
6. Join B3C.
7. Through B4 draw a line B4C’ parallel to B3C, intersecting the extended line segment BC at C’.
8. Through C’, draw a line A’C’ parallel to CA, intersecting the extended line segment BA at A’.
Thus, A’BC’ is the required triangle.
Justification:

Question 7.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are times the corresponding sides of the given triangle.
Solution:
Steps of Construction:
1. Construct a ∆ABC, such that BC = 4 cm, CA = 3 cm and ∠BCA = 90°
2. Draw a ray BX making an acute angle with BC.
3. Mark five points B1, B2, B3, B4 and B5 on BX, such that BB1 = B1B2 = B2B3 = B3B4 = B4B5.
4. Join B3C.
5. Through B5, draw B5C’ parallel to B3C intersecting BC produced at C’.
6. Through C’, draw C’A’ parallel to CA intersecting AB produced at A’.
Thus, ∆A’BC’ is the required right triangle.

Justification:

Exercise 11.2
Question 1.
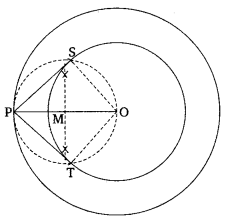
Draw a circle of radius 6 cm. From a point 10 cm away from its center, construct the pair of tangents to the circle and measure their lengths.
Solution:
Steps of Construction:
1. Draw a circle with center and radices = 6 cm.
2. Take a point P such that OP = 10 cm.
3. Draw the perpendicular bisector of OP. Let M is the mid-point of OP.
4. With center M and radius PM = MO, draw a circle which cuts the given circle at S and T.
5. Join PS and PT.
Thus, PS and PT are the required tangents.
The length of tangents Ps= PT = 8 cm.

Justification:

Question 2.
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also, verify the measurement by actual calculation.
Solution:
Steps of Construction:
1. Draw two given concentric circles of radii 4 cm and 6 cm with common center O.
2. Take a point P on the circumference of a bigger circle and join OP
3. Mark the mid-point M of OP by drawing perpendicular bisector of it.
4. With center Mand radius MP = OM. draw a circle which intersects the smaller circle at S and T.
5. Join PS and PT.
Thus, PS and PT are the required tangents to the smaller circle.
On measuring PS = PT = 4.4 cm (app.)
Justification:
Join OS. In ∆PSO, ∠PSO = 90°

Question 3.
Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its center. Draw tangents to the circle from these two points P and Q.
Solution:
Steps of Construction:
1. With center and radius 3 cm, draw a circle.
2. Produce the diameter of the circle to both the ends up to P and such that OP = OQ = 7 cm
3. Mark the mid-points M and M’ of the OP and OQ respectively
4. With centers M and M’ and radii MP and MO respectively, draw two circles.
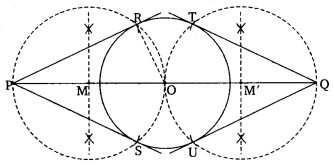
5. Circle with center M intersects the given circle at Rand S. The circle with center M intersects the given circle at T and U.
6. Join PR, PS, QT, and QU.
Thus, we have PR and PS as a pair of tangents from P and OT and QU as another pair of tangents from Q drawn to the given circle.
Justification:
Join OR. Now in ∆PRO,
∠PRO = 90° [Angle in a semicircle]
Also, OR is the radius of the circle with center O.
∴ Line PR⊥ OR.
We know that a line drawn through the end of a radius and perpendicular to it is a tangent to the circle.
Hence, PR is the tangent to the point R similarly, PS, QT, and QU are the tangents at the points S, T and U respectively.
Question 4.
Draw a pair of tangents to a circle of radius 5 cm which is inclined to each other at an angle of 60°.
Solution:
Steps of Construction:
1. Draw a circle with center and radius 5 cm.
2. Draw two radial OQ and OR, such that ∠QOR = 120°
3. Draw perpendiculars to OQ and OR, which intersect each other at a point P.
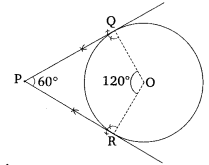
Thus, PQ and PR are the required tangents which are inclined at 60°.
Question 5.
Draw a line segment AB of length 8 cm. Taking A as a center, draw a circle of radius 4 cm and taking B as a center, draw another circle of radius 3 cm. Construct tangents to each circle from the center of the other circle.
Solution:
Steps of Construction:
1. Draw a line segment AB = 8 cm.
2. With centers A and B and radial 4 cm and 3 cm respectively draw two circles.
3. Mark the mid-point M of AB,
4. With center M and radius AM = BM, draw a circle intersecting the two circles at P, Q, and R, S.
5. Join AP, AQ, BR, and BS.
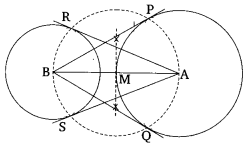
Thus, AR and AS are a pair of tangents drawn from A to the given circle, and BP and BO are a pair of tangents drawn from B to the given circle.
Question 6.
Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠B = 90°. BD is the perpendicular Burn B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Solution:
Steps of Construction:
1. Construct a right triangle ABC, such that AB = 6 cm, BC = 8 cm and ∠ABC = 90°.
2. Mark the mid-point of BC as O.
3. Join OA.
4. With O as a center and OB radius, draw a circle which intersects the side AC of ∆ABC at D.
5. Join BD, which cuts OA at M.
6. With center M and radius MA – BM, draw a circle intersecting the first circle at B and E.
7. Join AB and AE.
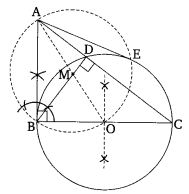
Thus, AB and AE are the required tangents
dawn from point A
Question 7.
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.
Solution:
Steps of Construction:
1. Draw a circle with the bangle.
2. Take two non-parallel chords AB and CD of the circle
3. Draw perpendicular bisectors of these chords intersecting each other at O, which is the center of the circle.
4. Take a point P outside the circle.
5. Join OP.
6. Mark the mid-point M of OP.
7. With M as center and radius equal to MP = OM, draw a circle intersecting the first circle at and R.
8. Join PQ and PR.
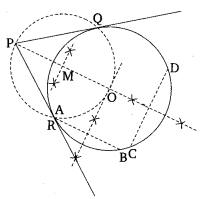
Thus, PQ and PR are the required tangents.