GetStudySolution

Getstudysolution is an online educational platform that allows students to access quality educational services and study materials at no cost.

NCERT Solutions for class 7 Maths chapter 14 – Symmetry

Back Exercise

Exercise 14.1

Question 1.
Copy the figures with punched holes and find the axes of symmetry for the following :


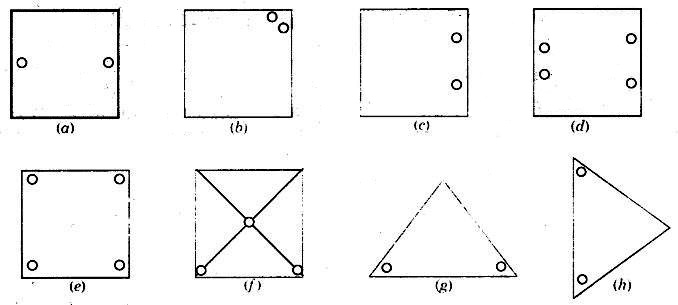
Solution:

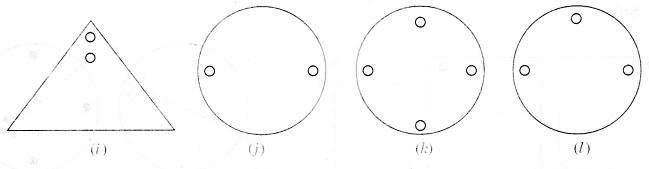
Question 2.
Given the line(s) of symmetry, find the other hole(s):

Solution:

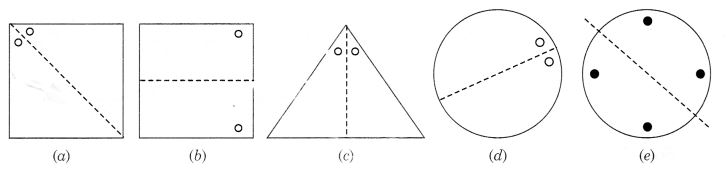
Question 3.
In the following figures, the mirror line (i.e., the line of symmetry) is given as a dotted line. Complete each figure performing reflection in the dotted (mirror) line. (You might perhaps place a mirror along the dotted line and look into the mirror for the image). Are you able to recall the name of the figure you complete?
<
Solution:

Question 4.
The following figures have more than one line of symmetry. Such figures are said to have multiple lines of symmetry:

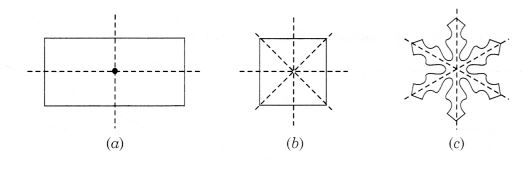
Identify multiple lines of symmetry, if any, in each of the following figures:

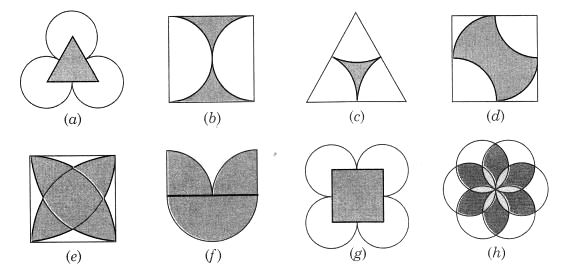
Solution:

Question 5.
Copy the figure given here. Take any one diagonal as a line of symmetry and shade a few more squares to make the figure symmetric about a diagonal. Is there more than one way to do that? Will the figure be symmetric about both the diagonals?

Solution:


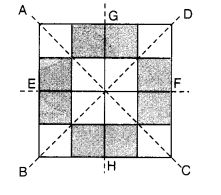
Yes! there is more than one way to make the figure symmetric.

• Let us take the diagonal BD and shade the squares as shown in the figure to make the figure symmetric about BD.
• Similarly, the figure is symmetric about the diagonal AC. Thus, the figure is symmetric about both the diagonals.
• The figure is symmetric about EF and GH also.

Question 6.
Copy the diagram and complete each shape to be symmetric about the mirror line(s) :

Solution:

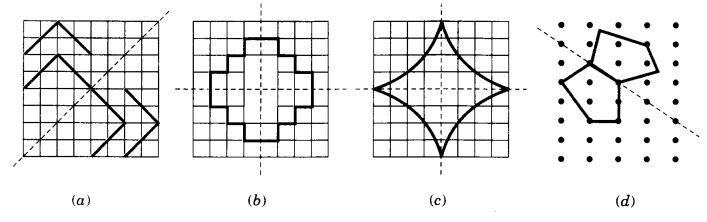
Question 7.
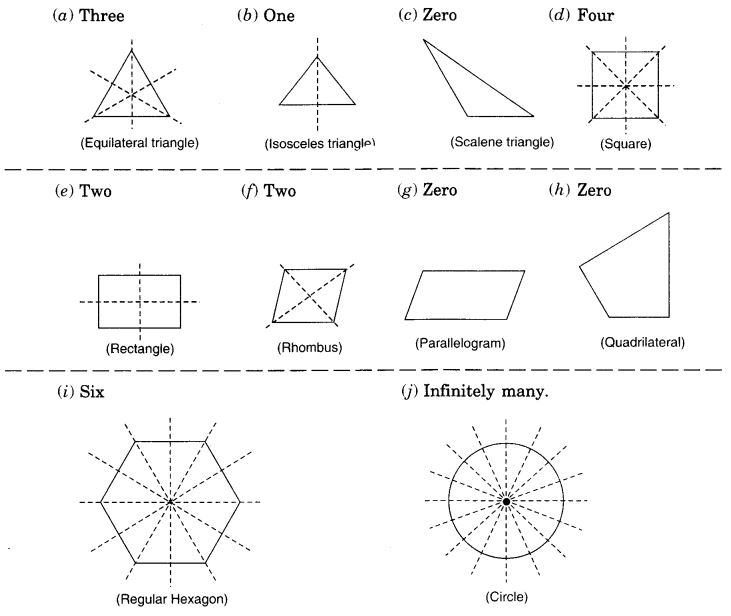
State the number of lines of symmetry for the following figures :
(a) An equilateral triangle
(b) An isosceles triangle
(c) A scalene triangle
(d) A square
(e) A rectangle
(f) A rhombus
(g) A parallelogram
(h) A quadrilateral
(i) A regular hexagon
(j) A circle.
Solution:

Question 8.
What letters of the English alphabet have reflectional symmetry (i.e., symmetry related to mirror reflection) about
(a) a vertical mirror
(b) a horizontal mirror
(c) both horizontal and vertical mirrors.
Solution:

Question 9.
Give three examples of shapes with no line of symmetry.
Solution:

(b) A scalene triangle,
(c) A parallelogram

Question 10.
What other name can you give to the line of symmetry of

1. an isosceles triangle?
2. a circle?

Solution:

1. Median
2. Diameter

Exercise 14.2

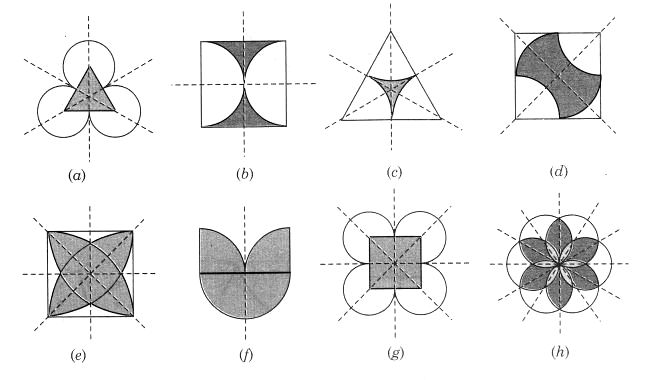
Question 1.
Which of the following figures have rotational symmetry of order more than 1?

Solution:
Figures (a), (b), (d), (e) and (f) have rotational symmetry of order more than 1.

Question 2.
Give the order of rotational symmetry for each figure :


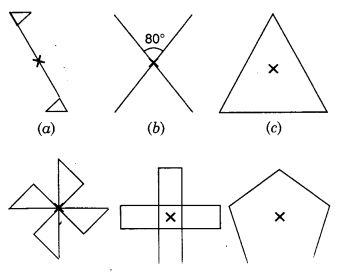
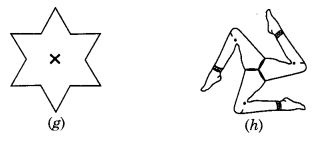
Solution:

(a) → 2
(b) → 2
(c) → 3
(d) → 4
(e) → 4
(f) → 5
(g) → 6
(h) → 3

Mark a point P as shown in figure (i). We see that in a full turn, there are two positions (on rotation through the angles 180° and 360°) when the figure looks exactly the same. Because of this, it has rotational symmetry of order 2.

Mark a point P as shown in figure (i). We see that in a full turn, there are two positions (on rotation through the angles 180° and 360°) when the figure looks exactly the same.

Because of this, it has rotational symmetry of order 2.

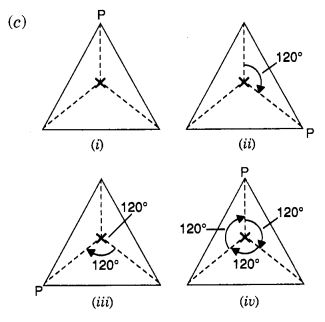
Mark a point P as shown in figure (i). We see that in a full turn, there are three positions (on rotation through the angles 120°, 240°, and 360°) when the figure looks exactly the same. Because of this, it has rotational symmetry of order 3.

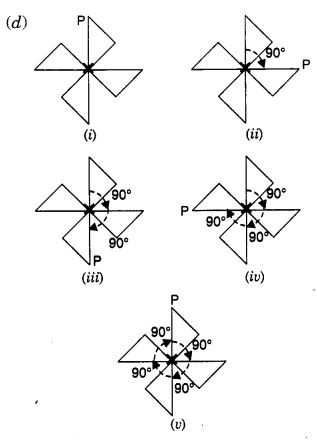
Mark a point P as shown in figure (i). We see that in a full turn, there are four positions (on rotation through the angles 90°, 180°, 270°, and 360°) when the figure looks exactly the same. Because of this, we say that it has rotational symmetry of order 4.

Similarly,

(e) In a full turn, there are four positions (on rotation through the angles 90°, 180°, 270°, and 360°) when the figure looks exactly the same.

∴ It has rotational symmetry of order 4.

(f) The figure is a regular pentagon. In a full turn, there are five positions (on rotation through the angles 72°, 144°, 216°, 288°, and 360°) when the figure looks exactly the same.

∴ It has rotational symmetry of order 5.

(g) In a full turn, there are six positions (on rotation through the angles 60°, 120°, 180°, 240°, 300°, and 360°) when the figure looks exactly the same.

It has rotational symmetry of order 6.

(h) In a full turn, there are three positions (on rotation through the angles 120°, 240°, and 360°) when the figure looks exactly the same.

∴ It has rotational symmetry of order 3.

Exercise 14.3

Question 1.
Name any two figures that have both line symmetry and rotational symmetry.
Solution:
Two figures that have both line symmetry and rotational symmetry are an equilateral triangle and a circle.

Question 2.
Draw, wherever possible, a rough sketch of
(i) a triangle with both line and rotational symmetry of order more than 1.
(ii) a triangle with only line symmetry and no rotational symmetry of order more than 1.
(iii) a quadrilateral with rotational symmetry of order more than 1 but not a line symmetry.
(iv) a quadrilateral with line symmetry but not a rotational symmetry of order more than 1.
Solution:
(i) An equilateral triangle has 3 lines of symmetry and rotational symmetry of order 3.


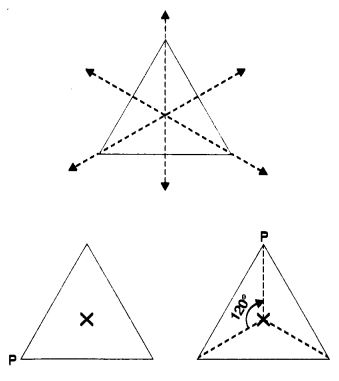
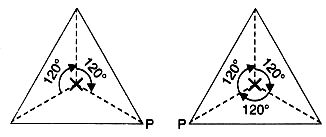
(ii) An isosceles triangle has only one line symmetry but no rotational symmetry of order more than 1.

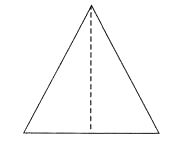
(iii) A parallelogram has no line of symmetry but has a rotational symmetry of order 2.

(iv) An isosceles trapezium has one line of symmetry but no rotational symmetry of order more than 1.

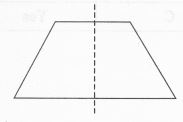
Question 3.
If a figure has two or more lines of symmetry, should it have rotational symmetry of order more than 1?
Solution:
When a figure has two or more lines of symmetry, then the figure should have rotational symmetry of order more than 1.

Question 4.
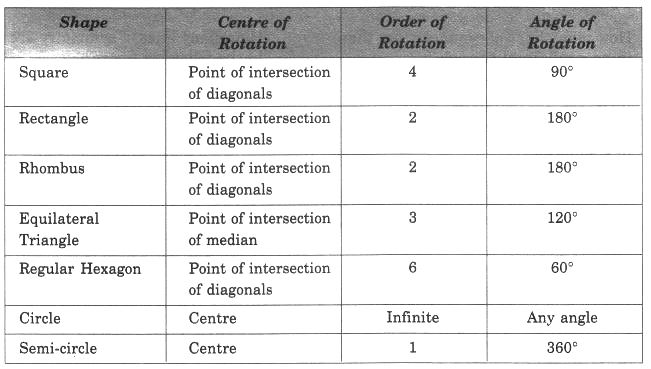
Fill in the blanks:

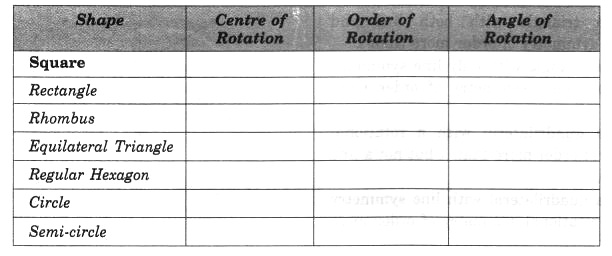
Solution:

Question 5.
Name the quadrilaterals which have both line and rotational symmetry of order more than 1.
Solution:
The name of quadrilaterals having both line and rotational symmetry is square.

Question 6.
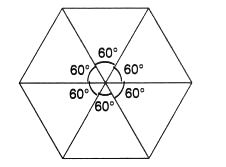
After rotating by 60° about a centre, a figure looks exactly the same as its original position. At what other angles will this happen for the figure?
Solution:
The other angles are 120°, 180°, 240°, 300°, and 360°.

Question 7.
Can we have a rotational symmetry of order more than 1 whose angle of rotation is
(i) 45°?
(ii) 17°?
Solution:
(i) Yes

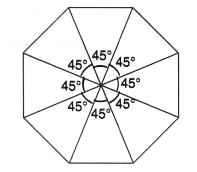
(ii) No