GetStudySolution

Getstudysolution is an online educational platform that allows students to access quality educational services and study materials at no cost.

NCERT Solutions for class 9 Maths chapter 2 – Polynomials

Back Exercise

Exercise 2.1

Question 1.
Which of the following expressions are polynomials in one variable and which are not? State reasons for your answer.
(i) 4x² – 3x + 7
(ii) y² + √2
(iii) 3 √t + t√2
(iv) y+ $\frac { 2 }{ y }$
(v) x¹⁰+ y³+t⁵⁰
Solution:
(i) 4x² – 3x + 7 is an expression having only non-negative integral powers of x. So, it is a polynomial.
(ii) y² +√2 is an expression having only non-negative integral power of y. So, it is a polynomial.
(iii) 3√t + √2 is an expression in which one term namely 3√t has rational power of f. So, it is not a polynomial.
(iv) y+ $\frac { 2 }{ y }$ is an expression in which one term namely $\frac { 2 }{ y }$ ⇒ i.e., 2y^-1 has negative power of y. So, it is not a polynomial.
(v) x¹⁰ + y³ + t⁵⁰ is an expression which has 3 variables.

Question 2.
Write the coefficients of x² in each of the following
(i) 2 + x² + x
(ii) 2 – x2 + x3
(iii) $\frac { \pi }{ 2 }$ x² + x
(iv) √2 x – 1
Solution:
(i) The coefficient of x² in 2 + x² + x is 1.
(ii) The coefficient of x² in 2 – x² + x³ is – 1.
(iii) The coefficient of x² in $\frac { \pi }{ 2 }$ x²+ x is $\frac { \pi }{ 2 }$ .
(iv) The coefficient of x² in √2 x -1 is 0.

Question 3.
Give one example each of a binomial of degree 35, and of a monomial of degree 100.
Solution:
(i) y³⁵ + 2 is a binomial of degree 35.
(ii) y¹⁰⁰ is a monomial of degree 100.

Question 4.
Write the degree of each of the following polynomials.
(i) 5x³+4x² + 7x
(ii) 4 – y²
(iii) 5f – √7
(iv) 3
Solution:
(i) In a polynomial 5x³ + 4x² + 7x, the highest power of variable x is 3, hence degree of polynomial is 3.
(ii) In a polynomial 4 – y², the highest power of variable y = 2, hence degree of polynomial is 2.
(iii) In a polynomial 5t – √7 , the highest power of variable t = 1, hence the degree of polynomial is 1.
(iv) In a polynomial 3, the highest power of variable y = 0, hence the degree of polynomial is 0.

Question 5.
Classify the following as linear, quadratic and cubic polynomials.
(i) x²+ x
(ii) x – x³
(iii) y + y²+4
(iv) 1 + x
(v) 3t
(vi) r²
(vii) 7x³
Solution:
(i) The degree of polynomial x² + 2 is 2, hence it is a quadratic polynomial.
(ii) The degree of polynomial x – x³ is 3, hence it is a cubic polynomial.
(iii) The degree of polynomial y + y² + 4 is 2, hence it is a quadratic polynomial.
(iv) The degree of polynomial 1 + x is 1, hence it is a linear polynomial.
(v) The degree of polynomial 3t is 1, hence it a linear polynomial.
(vi) The degree of polynomial r² is 2, hence it is a quadratic polynomial.
(vii) The degree of polynomial 7x³ is 3, hence it is a cubic polynomial.

Exercise 2.2

Question 1.
Find the value of the polynomial 5x -4x² + 3 at
(i) x = 0
(ii) x = – 1
(iii) x = 2
Solution:
Let p (x) = 5x – 4x²+ 3
(i) The value of p (x) = 5x – 4x²+ 3 at x= 0 is
p(0) = 5 x 0 – 4 x 0²+3
⇒ P (0) = 3
(ii) The value of p (x) = 5x – 4x² + 3 at x = -1 is
p(-1) = 5(-D-4(-1)² + 3 = – 5 -4 + 3
⇒ P(-1) = -6
(iii) The value of p (x) = 5x- 4x² + 3 at x = 2 is
p (2) = 5 (2)- 4 (2)² + 3= 10- 16+ 3
⇒ P (2) = – 3

Question 2.
Find p (0), p (1) and p (2) for each of the following polynomials.
(i) p(y) = y² – y +1
(ii) p (t) = 2 +1 + 2t² -t³
(iii) P (x) = x³
(iv) p (x) = (x-1) (x+1)
Solution:
(i) p (y) = y² -y +1
∴ p(0) = 0²-0+1
⇒ p(0) = 1
p(1) = 1²-1+ 1
⇒ p(1) = 1
and p (2) = 2² – 2 + 1 =4-2+1
⇒ P (2) = 3
(ii) p (t) = 2 + t + 2t² -1³
p(0) = 2+ 0+ 2 x 0²– 0³
⇒ P (0) = 2
p (1) = 2 + 1 + 2 x 1² – 1³
⇒ p (1) = 3 + 2 – 1
⇒ p(1) = 4
and p (2) = 2 + 2 + 2 x 2² – 2³
=4+8-8
⇒ P (2) = 4
(iii) P(x) = x³
⇒ p (0) = 0³ ⇒ p (0) = 0 ⇒ p (1) = 1³
⇒ P (1) = 1
and p (2) = 2³ ⇒ p (2) = 8
(iv) p(x) = (x-1)(x+ 1)
p(0) = (0-1)(0+1)
⇒ P (0) = – 1
p (1) = (1 – 1) (1 + 1)
⇒ P (1) = 0
and p (2) = (2-1) (2+1)
⇒ P (2) = 3

Question 3.
Verify whether the following are zeroes of the polynomial, indicated against them.
(i)p(x) = 3x + 1,x = –$\frac { 1 }{ 3 }$
(ii)p (x) = 5x – π, x = $\frac { 4 }{ 5 }$
(iii) p (x) = x² – 1, x = x – 1
(iv) p (x) = (x + 1) (x – 2), x = – 1,2
(v) p (x) = x², x = 0
(vi) p (x) = lx + m, x = – $\frac { m }{ l }$
(vii) P (x) = 3x² – 1, x = – $\frac { 1 }{ \sqrt { 3 } }$,$\frac { 2 }{ \sqrt { 3 } }$
(viii) p (x) = 2x + 1, x = $\frac { 1 }{ 2 }$
Solution:

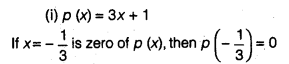
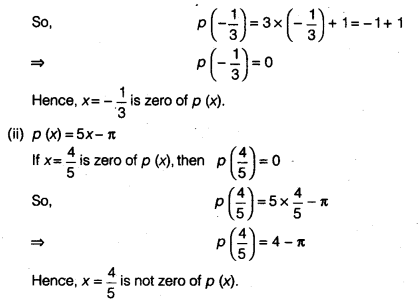
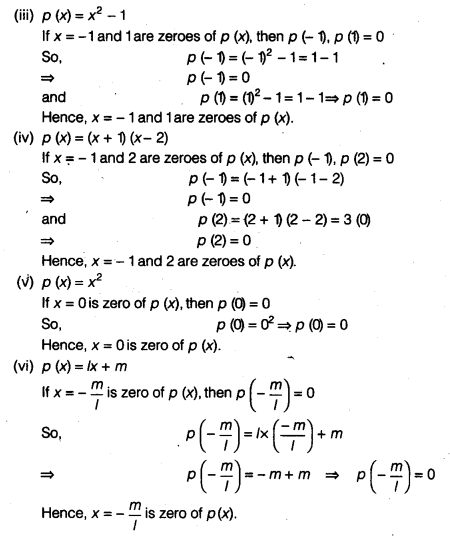
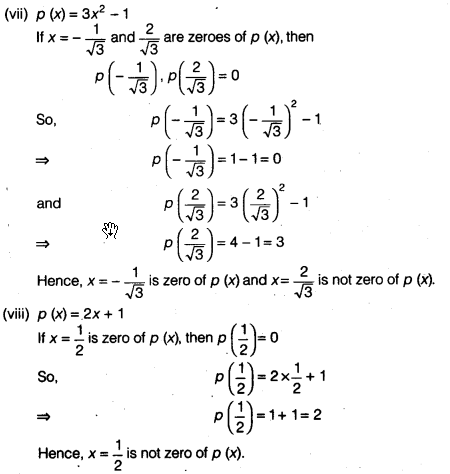
Question 4.
Find the zero of the polynomial in each of the following cases
(i) p(x)=x+5
(ii) p (x) = x – 5
(iii) p (x) = 2x + 5
(iv) p (x) = 3x – 2
(v) p (x) = 3x
(vi) p (x)= ax, a≠0
(vii) p (x) = cx + d, c≠ 0 where c and d are real numbers.
Solution:
(i) We have, p (x)= x+ 5
Now, p (x) = 0
⇒ x+ 5 = 0
⇒ x = -5
∴ – 5 is a zero of the polynomial p (x).
(ii) We have, p (x) = x – 5
Now, p (x) = 0
⇒ x – 5 = 0
⇒ x = 5
∴ 5 is a zero of the polynomial p (x).
(iii) We have, p (x) = 2x + 5
Now, P (x)= 0
⇒ 2x+ 5= 0
⇒ x = –$\frac { 5 }{ 2 }$
∴ –$\frac { 5 }{ 2 }$ is a zero of the polynomial p (x).
(iv) We have, p (x)= 3x- 2
Now p(x) = 0
⇒ 3x- 2 = 0
⇒ x= $\frac { 2 }{ 3 }$
∴ $\frac { 2 }{ 3 }$ is a zero of the polynomial p (x).
(v) We have, p (x) = 3x
Now, p (x)= 0
⇒ 3x=0
⇒ x =0
∴ 0 is a zero of the polynomial p (x).
(vi) We have, p (x)= ax, a ≠ 0
Now, p (x)= 0 ⇒ ax= 0
⇒ x= 0
∴ 0 is.a zero of the polynomial p (x).
(vii) We have, p (x) = cx + d,c ≠ 0
Now, p (x) = 0
⇒ cx + d = 0
x = – $\frac { d }{ c }$
∴ – $\frac { d }{ c }$ is a zero of the polynomial p (x).

Exercise 2.3

Question 1.
Find the remainder when x³ + 3x² + 3x + 1 is divided by
(i) x + 1
(ii) x – $\frac { 1 }{ 2 }$
(iii) x
(iv) x + π
(v) 5 + 2x
Solution:
Let p (x) = x³ + 3x² + 3x + 1
(i) The zero of x+ 1 is – 1. (∵ x+ 1 = 0= x = -1)

Question 2.
Find the remainder when x³-ax² +6x-ais divided by x – a.
Solution:
The zero of x – a is a. (∵ x – a = 0 =» x= a)
Let p (x) = x³ – ax² + 6x – a
So, p (a) = a³ – a (a)² + 6a – a = a³ – a³ + 5a
⇒ p (a) = 5a
∴ Required remainder = 5a (By Remainder theorem)

Question 3.
Check whether 7 + 3x is a factor of 3x³+7x.
Solution:
Let f(x) = 3x³+7x

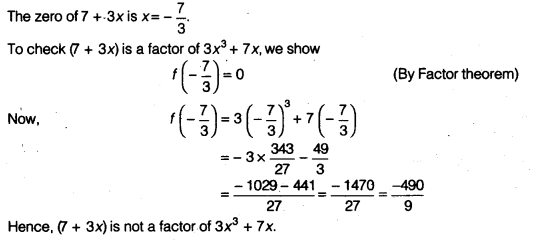
Exercise 2.4

Question 1.
Determine which of the following polynomials has (x +1) a factor.
(i) x³+x²+x +1
(ii) x⁴ + x³ + x² + x + 1
(iii) x⁴ + 3x³ + 3x² + x + 1
(iv) x³ – x² – (2 +√2 )x + √2
Solution:
The zero of x + 1 is -1.
(i) Let p (x) = x³ + x² + x + 1
Then, p (-1) = (-1)³ + (-1)² + (-1) + 1 .
= -1 + 1 – 1 + 1
⇒ p (- 1) = 0
So, by the Factor theorem (x+ 1) is a factor of x³ + x² + x + 1.
(ii) Let p (x) = x⁴ + x³ + x² + x + 1
Then, P(-1) = (-1)⁴ + (-1)³ + (-1)² + (-1)+1
= 1 – 1 + 1 – 1 + 1
⇒ P (-1) = 1
So, by the Factor theorem (x + 1) is not a factor of x⁴ + x³ + x² + x+ 1.
(iii) Let p (x) = x⁴ + 3x³ + 3x² + x + 1 .
Then, p (-1)= (-1)⁴ + 3 (-1)³ + 3 (-1)² + (- 1)+ 1
= 1- 3 + 3 – 1 + 1
⇒ p (-1) = 1
So, by the Factor theorem (x + 1) is not a factor of x⁴ + 3x³ + 3x² + x+ 1.
(iv) Let p (x) = x³ – x² – (2 + √2) x + √2
Then, p (- 1) =(- 1)3- (-1)2 – (2 + √2)(-1) + √2
= -1 – 1+ 2 +√2+√2
= 2√2
So, by the Factor theorem (x + 1) is not a factor of
x³ – x² – (2 + √2) x + √2.

Question 2.
Use the Factor Theorem to determine whether g (x) is a factor of p (x) in each of the following cases
(i) p (x)= 2x³ + x² – 2x – 1, g (x) = x + 1
(ii) p(x)= x³ + 3x² + 3x + X g (x) = x + 2
(iii) p (x) = x³ – 4x² + x + 6, g (x) = x – 3
Solution:
(i) The zero of g (x) = x + 1 is x= -1.
Then, p (-1) = 2 (-1)³+ (-1)² – 2 (-1)-1 [∵ p(x) = 2x³ + x² – 2x -1]
= -2 + 1 + 2 – 1
⇒ P (- 1)= 0
Hence, g (x) is a factor of p (x).

(ii) The zero of g (x) = x + 2 is – 2.
Then, p (- 2) = (- 2)³ + 3 (- 2)² +3 (- 2) + 1 [∵ p(x) = x³ + 3x² + 3x + 1]
= – 8 + 12 – 6 + 1
⇒ p(-2) = -1
Hence, g (x) is not a factor of p (x).

(iii) The zero of g (x) = x – 3 is 3.
Then, p (3) = 3³ – 4 (3)²+3 + 6 [∵ p(x) = x³-4x² + x+6]
= 27 – 36+ 3 +6
⇒ p(3) = 0
Hence, g (x) is a factor of p (x).

Question 3.
Find the value of k, if x – 1 is a factor of p (x) in each of the following cases
(i) p (x) = x² + x + k
(ii) p (x) = 2x² + kx + √2
(iii) p (x) = kx² – √2 x + 1
(iv) p (x) = kx² – 3x + k
Solution:
The zero of x – 1 is 1.
(i) (x – 1) is a factor of p (x),then p(1)= 0 (By Factor theorem)
⇒ 1² + 1 + k = 0 [∵ p(x) = x² + x + k]
⇒ 2 + k =0
⇒ k = -2
(ii) ∵ (x -1) is a factor of p (x), then p (1) = 0 (By Factor theorem)
⇒ 2(1)² + k(1)+√2= 0 [∵p(x) = 2x² + kx+ -√2]
⇒ 2 + k + √2 = 0
⇒ k = – (2 + √2)
(iii) ∵ (x-1) is a factor of p (x), then p (1) = 0 (By Factor theorem)
⇒ k (1)² – √2 + 1 = 0 [∵p(x) = kx² – √2x + 1]
⇒ k = (√2 – 1)
(iv) ∵ (x-1) is a factor of p (x), then p (1) = 0 (By Factor theorem)
⇒ k(1)² – 3 + k = 0 [∵p(x) = kx² – 3x + k]
⇒ 2k-3 = 0
⇒ k = $\frac { 3 }{ 2 }$

Question 4.
Factorise
(i) 12x² – 7x +1
(ii) 2x² + 7x + 3
(iii) 6x² + 5x – 6
(iv) 3x² – x – 4
Solution:
(i) 12x² – 7x + 1 = 12x² – 4x- 3x + 1 (Splitting middle term)
= 4x (3x – -0 -1 (3x-1)
= (3x -1) (4x -1)
(ii)2x² + 7x + 3 = 2x² + 6x + x + 3 (Splitting middle term)
= 2x (x + 3) +1 (x + 3) = (x + 3) (2x+ 1)
(iii) 6x² + 5x – 6= 6x² + 9x- 4x- 6 (Splitting middle term)
= 3x(2x+3)-2(2x+3)=(2x+3)(3x-2)
(iv) 3x² – x- 4= 3x²-4x+3x-4 (Splitting middle term)
= x (3x – 4) + 1 (3x – 4)= (3x- 4) (x + 1)

Question 5.
Factorise
(i) x³ – 2x² – x + 2
(ii) x³ – 3x² – 9x – 5
(iii) x³ + 13x² + 32x + 20
(iv) 2y³ + y² – 2y – 1
Solution:
(i) Let p (x) = x³ – 2x² – x+ 2, constant term of p (x) is 2.
Factors of 2 are ± 1 and ± 2.
Now, p (1) = 1³ – 2 (1)² – 1 + 2
=1- 2 – 1 + 2
p(1) = 0
By trial, we find that p (1) = 0, so (x – 1) is a factor of p (x).
So, x³ – 2x² – x+ 2
= x³ – x² – x² + x – 2x + 2
= x² ( x -1)- x (x – 1)-2 (x – 1)
= (x – 1)(x² – x – 2)
= (x – 1)(x² – 2x+x-2)
= (x – 1) [x (x – 2) + 1 (x – 2)]
= (x – 1) (x – 2)(x + 1)

(ii) Let p(x) = x³ – 3x² – 9x – 5
By trial, we find that p(5) = (5)³ – 3(5)² – 9(5) – 5
=125 – 75 – 45 – 5 = 0
So, (x – 5) is a factor of p(x).
So, x³ – 3x² – 9x – 5
= x³-5x² + 2x²-10x+x-5
= x²(x – 5)+2x(x – 5)+1(x – 5)
= (x – 5) (x² + 2x + 1)
= (x – 5) (x² + x + x + 1)
= (x – 5) [x (x + 1)+ 1 (x+ 1)]
= (x – 5) (x + 1) (x + 1)
= (x – 5)(x+1)²

(iii) Let p (x) = x³ + 13x² + 32x + 20
By trial, we find that p (-1) = (-1)³ + 13(-1)² + 32 (-1) + 20
= -1+13 – 32 + 20 = -33 + 33 = 0
So (x + 1) is a factor of p (x).
So, x³ + 13x² + 32x + 20
= x³+ x² + 12x² + 12x+ 20x+ 20
=x²(x+ 1) + 12x(x+ 1)+ 20 (x+ 1)
= (x+1)(x²+12x+20)
= (x+ 1) (x²+ 10x + 2x+ 20)
= (x+1)[x(x+10)+2(x+10)]
= (x+ 1) (x+ 10) (x + 2)

(iv) Let p (y) = 2y³ + y² – 2y -1
By trial we find that p(1) = 2 (1)³ + (1)² – 2(1) – 1 = 2 + 1 – 2 -1 = 0
So (y -1) is a factor of p (y).
So, 2y³ + y² – 2y -1
= 2y³ – 2y²+ 3y² – 3y + y – 1
= 2y²(y – 1) + 3y(y – 1)+1(y – 1)
= (y – 1) (2y² + 3y + 1)
= (y – 1)(2y² + 2y +y+1)
= (y – 1 [2y (y + 1) + 1 (y + 1)]
= (y – 1)(y+1)(2y+1)

Exercise 2.5

Question 1.
Use suitable identities to find the following products
(i) (x + 4)(x + 10)
(ii) (x+8) (x -10)
(iii) (3x + 4) (3x – 5)
(iv) (y²+ $\frac { 3 }{ 2 }$) (y²– $\frac { 3 }{ 2 }$)
(v) (3 – 2x) (3 + 2x)
Solution:
(i) (x+ 4) (x + 10)
Using identity (iv), i.e., (x+ a) (x+ b) = x² + (a + b) x+ ab.
We have, (x+4) (x + 10) = x²+(4 + 10) x + (4x 10) (∵ a = 4, b = 10)
= x² + 14x+40

(ii) (x+ 8) (x -10)
Using identity (iv), i.e., (x + a) (x + b) = x² + (a + b) x + ab
We have, (x + 8) (x – 10) = x² + [8 + (-10)] x + (8) (- 10)(∵a = 8, b = -10)
= x² – 2x – 80

(iii) (3x + 4) (3x – 5)
Using identity Eq. (iv), i.e.,
(x + a) (x + b) = x² + (a + b) x + ab
We have, (3x + 4) (3x – 5) = (3x)² + (4 – 5) x + (4) (- 5) (∵a = 4, b = -5)
= 9x² – x – 20

Question 2.
Evaluate the following products without multiplying directly
(i) 103 x 107
(ii) 95 x 96
(iii) 104 x 96
Solution:
(i) 103 x 107 = (100 + 3) (100 + 7)
= 100 x 100+ (3 + 7) (100)+ (3 x 7) [Using identity (iv)]
= 10000+ 1000+21 = 11021
(ii) 95 x 96 = (100-5) (100-4)
= 100 x 100 + [(- 5) + (- 4)] 100 + (- 5 x – 4) [Using identity (iv)]
= 10000 – 900 + 20 = 9120
(iii) 104 x 96 = (100 + 4) (100 – 4)
= (100)²-4² [Using identity (iii)]
= 10000-16 = 9984

Question 3.
Factorise the following using appropriate identities
(i) 9x²+6xy+ y²
(ii) 4y²-4y + 1
(iii) x² –$\frac { { y }^{ 2 } }{ 100 }$
Solution:

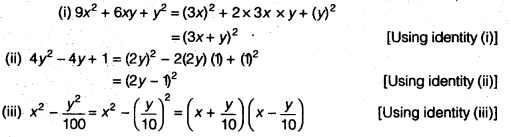
Question 4.
Expand each of the following, using suitable identity
(i) (x+2y+ 4z)²
(ii) (2x – y + z)²
(iii) (- 2x + 3y + 2z)²
(iv) (3a -7b – c)^z
(v) (- 2x + 5y – 3z)²
(vi) ( $\frac { 1 }{ 4 }$a –$\frac { 1 }{ 4 }$b + 1) ²
Solution:
(i) (x + 2y + 4z)² = x² + (2y)² + (4z)² + 2 (x) (2y) + 2 (2y) (4z) + 2(4z) (x) [Using identity (v)]
= x² + 4y² + 16z² + 4xy + 16yz + 8 zx
(ii) (2x – y + z)² = (2x)² + (- y)² + z² + 2 (2x) (- y)+ 2 (- y) (z) + 2 (z) (2x) [Using identity (v)]
= 4x² + y² + z² – 4xy – 2yz + 4zx
(iii) (- 2x + 3y + 2z)² = (- 2x)² + (3y)² + (2z)² + 2 (- 2x) (3y)+ 2 (3y) (2z) + 2 (2z) (- 2x) [Using identity (v)]
= 4x² + 9y² + 4z² – 12xy + 12yz – 8zx
(iv) (3a -7b- c)² = (3a)² + (- 7b)² + (- c)² + 2 (3a) (- 7b) + 2 (- 7b) (- c) + 2 (- c) (3a) [Using identity (v)]
= 9a² + 49b² + c² – 42ab + 14bc – 6ac
(v) (- 2x + 5y- 3z)² = (- 2x)² + (5y)² + (- 3z)² + 2 (- 2x) (5y) + 2 (5y) (- 3z) + 2 (- 3z) (- 2x) [Using identity (v)]
= 4x² + 25y² + 9z² – 20xy – 30yz + 12zx

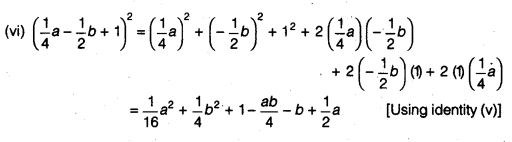
Question 5.
Factorise
(i) 4 x² + 9y² + 16z² + 12xy – 24yz – 16xz
(ii) 2x² + y² + 8z² – 2√2xy + 4√2yz – 8xz
Solution:
(i) 4x² + 9y² + 16z² +12xy-24yz-16xz
= (2x)² + (3y)² + (- 4z)² + 2 (2x) (3y) + 2 (3y) (- 4z) + 2 (- 4z) (2x)
= (2x + 3y – 4z)²
(ii) 2x² + y² + 8z² – 2√2xy + 4√2yz – 8xz
= (- √2x)² + (y)² + (2 √2z)² + 2(- √2x) (y)+ 2 (y) (2√2z) + 2 (2√2z) (- √2x)
= (- √2x + y + 2 √2z)²

Question 6.
Write the following cubes in expanded form

Solution:
(i) (2x + 1)³ = (2x)³ + 1³ + 3 (2x) (1) (2x + 1) [Using identity (x + y)³ = x³ + y³ + 3xy (x + y)]
= 8x³ + 1 + 6x (2x + 1)
= 8x³ + 1 + 12x² + 6x= 8x³ + 12x² + 6x + 1
(ii) (2a – 3b)³ = (2a)³ – (3b)³ -3(2a)(3b)(2a-3b) [Using identity (x-y)³=x³-y³ -3xy(x-y)]
= 8a³-27b³-18ab(2a-3b)
= 8a³ – 27 b³ – 36a²b + 54ab²
=8a³ – 36a²b + 54ab² – 27 b³

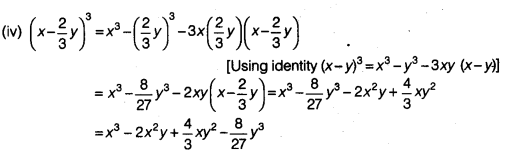
Question 7.
Evaluate the following using suitable identities
(i) (99)³
(ii) (102)³
(iii) (998)³
Solution:
(i) (99)³ =(100-1)³ = 100³ -(1)³ – 3x 100x 1(100-1) [Using identity (x-y)³ =x³-y³-3xy (x-y)]
=1000000-1-300(100-1)
=1000000-1-30000+300
=970299
(ii) (102)³ = (100+ 2)³ = 100³ + 2³ + 3x 100x 2 (100+ 2 [Using identity (x + y)³ = x³ + y³ + 3xy (x + y)]
=1000000 + 8 + 600(100+ 2)
=1000000 + 8 + 60000+ 1200=1061208
(iii) (998)³ = (1000-2)³ =1000³ – 2³ – 3x 1000x 2(1000-2) [Using identity (x-y)³=x³-y³-3xy (x-y)]
=1000000000-8-6000(1000-2)
= 1000000000- 8 – 6000000+12000
=994011992

Question 8.
Factorise each of the following
(i) 8a³ +b³ + 12a²b+6ab²
(ii) 8a³ -b³-12a²b+6ab²
(iii) 27-125a³ -135a+225a²
(iv) 64a³ -27b³ -144a²b + 108ab²

Solution:
(i) 8a³ +b³ +12a²b+6ab² = (2a)³ + b³ + 3x 2axb (2a+ b)
=(2a+b)³ [Using identity (vi)]
(ii) 8a³ -b³ -12a²b+ 6ab² = (2a)³ + (-b)³ + 3x2ax (-b)[(2a)+ (-b)]
= (2a)³ – (b)³ – 3 x 2ax b (2a-b) [Using identity (vii)]
=(2 a-b)³
(iii) 27-125a³-135a + 225a² =(3)³ + (-5a)³ + 3x3x(-5a)[(3)+(-5a)]
= (3)³ -(5a)³– 3x3x5a(3-5a) [Using identity (vii)]
= (3=5 a)³
(iv) 64a³ – 27b³ -144a²b +108ab² =(4a)³ + (-3b)³ + 3x4ax(-3b)[4a+ (-3b)]
=(4a)³-(3b)³-3x4ax3b(4a-3b)
=(4a-3b)³ [Using identity (vii)]

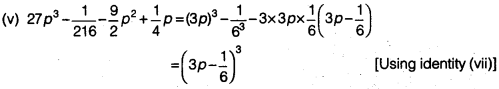
Question 9.
Verify
(i) x³ + y³ = (x + y)-(x² – xy + y²)
(ii) x³ – y³ = (x – y) (x² + xy + y²)
Solution:
(i) We know that,
(x + y)³ = x³ + y³ + 3xy (x + y)
⇒ x3 + y3 = (x + y)3 – 3xy (x + y)
= (x + y) [(x + y)² – 3xy]
= (x + y) [x² + y² + 2xy – 3xy]
= (x + y) [x² + y² – xy]
= RHS
Hence proved,
(ii) We .know that,
(x – y)³ = x³ – y³ – 3xy (x – y) x³ – y³
= (x – y)³ + 3xy (x – y)
= (x – y) [(x – y)² + 3xy]
= (x – y) [x² + y² + 2xy + 3xy]
= (x – y) [x² + y² + xy]
= RHS
Hence proved.

Question 10.
Factorise each of the following
(i) 27y³ + 125z
(ii) 64rh³ – 343n [Hint See question 9]
Solution:
(i) 27y³ + 125z³ = (3y)³ + (5z)³
= (3y + 5z) [(3y)² – (3y) (5z) + (5z)²]
= (3y + 5z) (9y² – 15yz + 25z²)
(ii) 64 m³ – 343 n³ = (4m)³ – (7n)³
= (4m – 7n) [(4m)² + (4m) (7n) + (7n)²]
= (4m – 7 n) [16m² + 28mn + 49n²]

Question 11.
Factorise 27x³ +y³ +z³ -9xyz.
Solution:
27x³ + y³ + z³-9xyz=(3x)³ + y³ + z³ -3x 3xx yx z
=(3x+y+z)[(3x)² + y² + z²– 3xy – yz -z(3x)][Using identity (viii)]
=(3x+ y + z) (9x² + y² + z² -3xy -yz -3zx)

Question 12.
Verify that
x³ +y³ +z³ -3xyz = $\frac { 1 }{ 2 }$ (x + y+z)[(x-y)² +(y-z)² +(z-x)²]
Solution:
x³ + y³ + z³-3xyz = (x+y+z)[x² + y² + z²-xy-yz-zx]
= $\frac { 1 }{ 2 }$(x+ y+ z)[2x² + 2y² + 2z² – 2xy- 2yz – 2zx]
= $\frac { 1 }{ 2 }$(x+y+z)[x² + x² + y² + y² + z² + z² – 2xy – 2yz – 2zx]
= $\frac { 1 }{ 2 }$(x+y+ z)[x² + y² – 2xy+ y² + z² – 2yz+ z² + x² -2zx]
= $\frac { 1 }{ 2 }$(x+y+z)[(x-y)² + (y-z)² + (z-x)²]

Question 13.
If x + y + z = 0, show that x³ + y³ + z³ = 3 xyz.
Solution:
We know that,
x³ + y³ + z³ – 3 xyz = (x + y + z) (x² + y² + z² – xy – yz – zx [Using identity (viii)]
= 0(x² + y² + z² – xy – yz – zx) (∵ x + y + z = 0 given)
= 0
⇒ x³ + y³ + z³ = 3 xyz
Hence proved.

Question 14.
Without actually calculating the cubes, find the value of each of the following
(i) (- 12)³ + (7)³ + (5)³
(ii) (28)³ + (- 15)³ + (- 13)³
Solution:
We know that, x³ + y³ + z³ -3xyz
=(x+y+z)(x² + y² + z² – xy – yz – zx)
If x+y+z=0, then x³ + y³ + z³-3xyz=0
or x³ + y³ + z³ = 3xyz
(i) We have to find the value of (-12)³ + (7)³ + (5)³
Here, -12+7+5=0
So, (-12)³ + (7)³ + (5)³= 3x(-12)(7)(5)
=-1260
(ii) We have to find the value of (28)³ + (-15)³ + (-13)³.
Here, 28+(-15)+(-13)=28-15-13 =0
So, (28)³ + (-15)³ + (-13)³
= 3x (28) (-15) (-13)
= 16380

Question 15.
Give possible expressions for the length and breadth of each of the following rectangles, in which their areas are given
(i) Area 25a² – 35a + 12
(ii) Area 35y² + 13y – 12
Solution:
(i) We have, area of rectangle
= 25a² – 35a+12
= 25a² – 20a – 15a+12
= 5a(5a – 4)-3(5a – 4)=(a-4)(5a – 3)
Possible expression for length =5a-3
and breadth =5a-4
(ii) We have, Area of rectangle = 35y²+13y – 12=35y² -15y + 28y – 12
=5y(7y – 3)+4(7y – 3) = (7y – 3)(5y+4)
Possible expression on for length =7y-3
and breadth =5y+4

Question 16.
What are the possible expressions for the dimensions of the cuboids whose volumes are given below?
(i) Volume 3x² – 12x
(ii) Volume 12ky² + 8ky – 20k
Solution:
(i) We have, volume of cuboid =3x²-12x=3x(x – 4)
One possible expressions for the dimensions of the cuboid is 3, x and x-4.
(ii) We have, volume of cuboid =12ky² + 8ky-20k
=12ky² + 20ky-12ky-20k
=4ky (3y+5) – 4k(3y+5)
=(3y+5)(4ky – 4k)
=(3y+5)4k(y – 1)
One possible expressions for the dimensions of the cuboid is 4k, 3y+5 and y – 1.