GetStudySolution

Getstudysolution is an online educational platform that allows students to access quality educational services and study materials at no cost.

NCERT Solutions for class 10 Maths chapter 2 – Polynomials

Back Exercise

Exercise 2.1

Question 1.
The graphs of y = p(x) are given in figure below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.

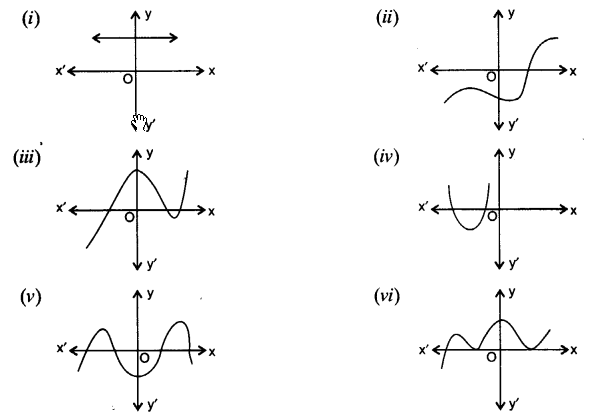
Solution:
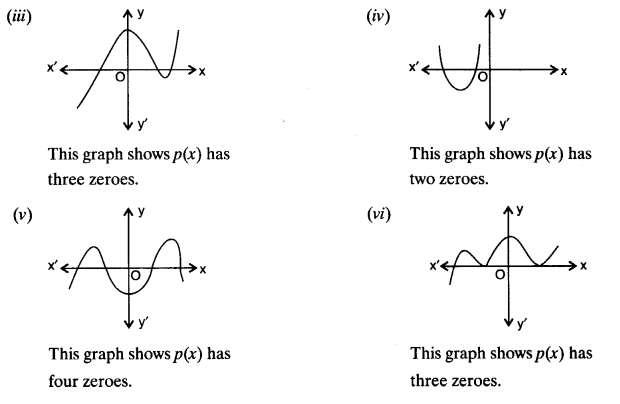
The number of zeroes of p(x) in each graph given; are

Exercise 2.2

Question 1.
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
(i) x² – 2x – 8
(ii) 4s² – 4s + 1
(iii) 6x² – 3 – 7x
(iv) 4u² + 8u
(v) t² -15
(vi) 3x² – x – 4
Solution:

Question 2.
Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.

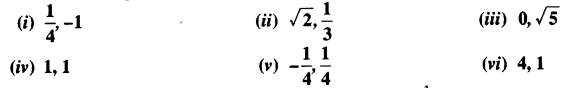
Solution:
(i) Zeroes of polynomial are not given, sum of zeroes = $\frac { 1 }{ 4 }$ and product of zeroes = -1
If ax² + bx + c is a quadratic polynomial, then
α + β = sum of zeroes = $\frac { -b }{ a }$ = $\frac { 1 }{ 4 }$ and αβ = product of zeroes = $\frac { c }{ a }$ = -1
Quadratic polynomial is ax² + bx + c
Let a = k, ∴ b = $\frac { -k }{ 4 }$ and c = -k
Putting these values, we get

For different values of k, we can have quadratic polynomials all having sum of zeroes as $\frac { 1 }{ 4 }$ and product of zeroes as -1.

(ii) Sum of zeroes = α + β = √2 = $\frac { -b }{ a }$; product of zeroes = αβ = $\frac { 1 }{ 3 }$ = $\frac { c }{ a }$
Quadratic polynomial is ax² + bx + c
Let a = k,b = -√2k and c = $\frac { k }{ 3 }$
Putting these values we get

For all different real values of k, we can have different quadratic polynomials of the form 3×2 – 3√2x +1 having sum of zeroes = √2 and product of zeroes = $\frac { 1 }{ 3 }$

(iii) Sum of zeroes = α + β = 0 = $\frac { -b }{ a }$; product of zeroes = αβ = √5 = $\frac { c }{ a }$
Let quadratic polynomial is ax² + bx + c
Let a = k,b = 0, c = √5 k
Putting these values, we get
k[x² – 0x + √5 ] = k(x² + √5).
For different real values of k, we can have different quadratic polynomials of the form
x² + √5, having sum of zeroes = 0 and product of zeroes = √5

(iv) Sum of zeroes = α + β = 1= $\frac { -b }{ a }$; product of zeroes = αβ = 1 = $\frac { c }{ a }$
Let quadratic polynomial is ax² + bx + c.
Let a=k, c = k, b = -k
Putting these values, we get k[x² -x +1]
Quadratic polynomial is of the form x² -x + 1 for different values of k.

(v) Sum of zeroes = α + β = $\frac { -1 }{ 4 }$= $\frac { -b }{ a }$; product of zeroes = αβ = $\frac { 1 }{ 4 }$ = $\frac { c }{ a }$
Let quadratic polynomial is ax² + bx + c
Let a=k, b= $\frac { k }{ 4 }$, c= $\frac { k }{ 4 }$
Putting these values, we get k

Quadratic polynomial is of the form 4x² +x + 1 for different values of k.

(vi) Sum of zeroes = α + β = 4 = $\frac { -b }{ a }$; product of zeroes = αβ = 1 = $\frac { c }{ a }$
Let quadratic polynomial is ax² + bx + c
Let a = k,b = -4k and c = k
Putting these values, we get
k[x² – 4x + 1]
Quadratic polynomial is of the form x² – 4x + 1 for different values of k.

Exercise 2.3

Question 1.
Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder, in each of the following:
(i) p(x) = x³ – 3x² + 5x -3, g(x) = x²-2
(ii) p(x) =x⁴ – 3x² + 4x + 5, g(x) = x² + 1 -x
(iii) p(x) = x⁴ – 5x + 6, g(x) = 2 -x²
Solution:
(i) Here p(x) = x³ -3x² + 5x – 3 and g(x) = x² -2
dividing p(x) by g(x) ⇒

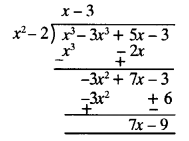
Quotient = x – 3, Remainder = 7x – 9

(ii) Here p(x) = x⁴– 3x² + 4x + 5 and g(x) = x² + 1 -x
dividing p(x) by g(x) ⇒

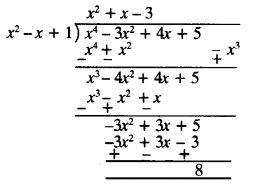
Quotient = x² + x – 3, Remainder = 8

(iii) Herep(x) = x⁴– 5x + 6 and g(x) = 2-x²
Rearranging g(x) = -x² + 2
dividing p(x) by g(x) ⇒
Quotient = -x² – 2
Remainder = -5x + 10.

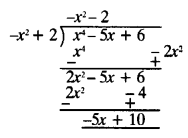
Question 2.
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
(i) t²-3, 2t⁴ + t³ – 2t² – 9t – 12
(ii) x² + 3x + 1,3x⁴+5x³-7x²+2x + 2
(iii) x³ -3x + 1, x⁵ – 4x³ + x² + 3x + l
Solution:
(i) First polynomial = t² – 3,
Second polynomial = 2t⁴ + 3t³ – 2t² – 9t – 12
dividing second polynomial
by first polynomial ⇒
∵ Remainder is zero.
∴First polynomial is a factor of second polynomial.

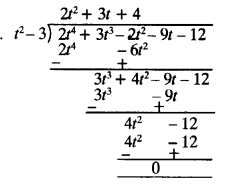
(ii) First polynomial = x² + 3x + 1
Second polynomial = 3x⁴ + 5x³ – 7x² + 2x + 2
dividing second polynomial
by first polynomial ⇒
∵ Remainder is zero.
∴ First polynomial is a factor of second polynomial.

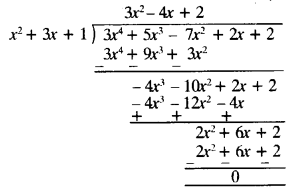
(iii) First polynomial = x³ – 3x + 1
Second polynomial = x⁵ – 4x³ + x² + 3x + 1.
∵ Remainder ≠ 0.
∴ First polynomial is not a factor of second polynomial.

Question 3.
Obtain all other zeroes of 3x⁴ + 6x³ – 2x² – 10x – 5, if two of its zeroes are $\sqrt { \frac { 5 }{ 3 } }$ and –$\sqrt { \frac { 5 }{ 3 } }$
Solution:

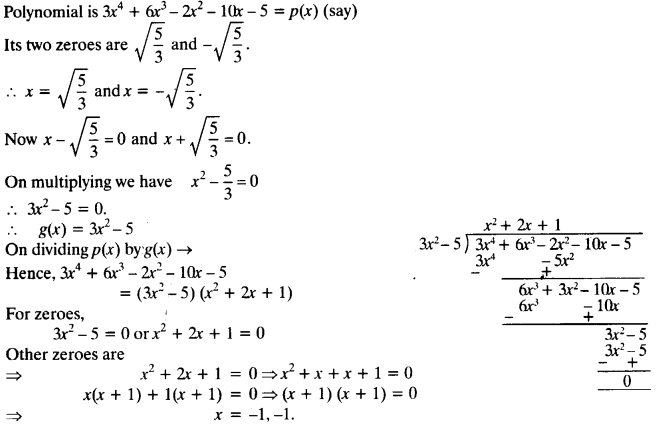
Question 4.
On dividing x³ – 3x² + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and -2x + 4, respectively. Find g(x).
Solution:
p(x) = x³ – 3 x 2 + x + 2 g(x) = ?
Quotient = x – 2; Remainder = -2x + 4
On dividing p(x) by g(x), we have
p(x) = g(x) x quotient + remainder
⇒ x³– 3x² + x + 2 = g(x) (x – 2) + (-2x + 4)
⇒ x³ – 3x² + x + 2 + 2 x- 4 = g(x) x (x-2)
⇒ x³ – 3x² + 3x – 2 = g(x) (x – 2)

Question 5.
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Solution:
(i) p(x),g(x),q(x),r(x)
deg p(x) = deg q(x)
∴ both g(x) and r(x) are constant terms.
p(x) = 2x²– 2x + 14; g(x) = 2
q(x) = x² – x + 7; r(x) = 0

(ii) deg q(x) = deg r(x)
∴ this is possible when
deg of both q(x) and r(x) should be less than p(x) and g(x).
p(x) = x³+ x² + x + 1; g(x) = x² – 1
q(x) = x + 1, r(x) = 2c + 2

(iii) deg r(x) is 0.
This is possible when product of q(x) and g(c) form a polynomial whose degree is equal to degree of p(x) and constant term.

Exercise 2.4

Question 1.
Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also, verify the relationship between the zeroes and the coefficients in each case:
(i) 2x³ + x² – 5x + 2;  $\frac { 1 }{ 4 }$, 1, -2
(ii) x³ – 4x² + 5x – 2; 2, 1, 1
Solution:
(i) Comparing the given polynomial with ax³ + bx² + cx + d, we get:
a = 2, b – 1, c = -5 and d = 2.
∴  p(x) = 2x³ + x² – 5x + 2


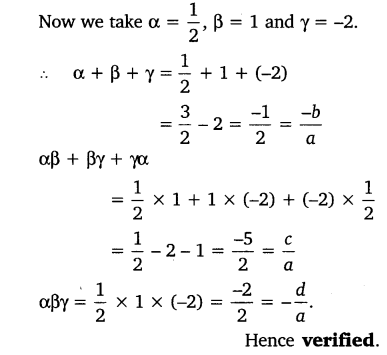
(ii) Compearing the given polynomial with ax³ + bx² + cx + d, we get:
a = 1, b = -4, c = 5 and d = – 2.
∴ p (x) = x³ – 4x² + 5x – 2
⇒  p(2) = (2)³ – 4(2)² + 5 x 2 – 2
= 8 – 16+ 10 – 2 = 0
p(1) = (1)³ – 4(1)² + 5 x 1-2
= 1 – 4 + 1 – 2
= 6-6 = 0
Hence, 2, 1 and 1 are the zeroes of x³ – 4x² + 5x – 2.
Hence verified.
Now we take α = 2, β = 1 and γ = 1.
α + β + γ = 2 + 1 + 1 = $\frac { 4 }{ 1 }$ = $\frac { -b }{ a }$
αβ + βγ + γα = 2 + 1 + 2 = $\frac { 5 }{ 1 }$ = $\frac { c }{ a }$
αβγ = 2 x 1 x 1  = $\frac { 2 }{ 1 }$ = $\frac { -d }{ a }$.
Hence verified.

Question 2.
Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, -7, -14 respectively.
Solution:
Let α , β and  γ be the zeroes of the required polynomial.
Then α + β + γ = 2, αβ + βγ + γα = -7 and αβγ = -14.
∴ Cubic polynomial
= x³ – (α + β + γ)x² + (αβ + βγ + γα)x – αβγ
= x³ – 2x² – 1x + 14
Hence, the required cubic polynomial is x³ – 2x² – 7x + 14.

Question 3.
If the zeroes of the polynomial x³ – 3x² + x + 1 are a-b, a, a + b, find a and b.
Solution:
Let α , β and  γ be the zeroes of polynomial x³ – 3x² + x + 1.
Then α =  a-b, β = a and γ = a + b.
∴ Sum of zeroes = α + β + γ
⇒   3 = (a – b) + a + (a + b)
⇒  (a – b) + a + (a + b) = 3
⇒  a-b + a + a + b = 3
⇒       3a = 3
⇒ a =  $\frac { 3 }{ 3 }$ = 1 …(i)
Product of zeroes = αβγ
⇒ -1 = (a – b) a (a + b)
⇒ (a – b) a (a + b) = -1
⇒   (a² – b²)a = -1
⇒  a³ – ab² = -1   … (ii)
Putting the value of a from equation (i) in equation (ii), we get:
(1)³-(1)b² = -1
⇒ 1 – b² = -1
⇒ – b² = -1 – 1
⇒  b² = 2
⇒ b = ±√2
Hence, a = 1 and b = ±√2.

Question 4.
If two zeroes of the polynomial x⁴ – 6x³ – 26x² + 138x – 35 are 2 ± √3, finnd other zeroes.
Solution:
Since two zeroes are 2 + √3 and 2 – √3,
∴  [x-(2 + √3)] [x- (2 – √3)]
= (x-2- √3)(x-2 + √3)
= (x-2)²– (√3)²
x² – 4x + 1 is a factor of the given polynomial.
Now, we divide the given polynomial by x² – 4x + 1.

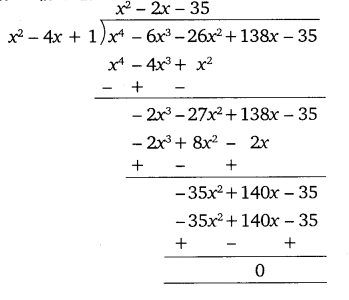
So, x⁴ – 6x³ – 26x² + 138x – 35
= (x² – 4x + 1) (x² – 2x – 35)
= (x² – 4x + 1) (x² – 7x + 5x – 35)
= (x²-4x + 1) [x(x- 7) + 5 (x-7)]
= (x² – 4x + 1) (x – 7) (x + 5)
Hence, the other zeroes of the given polynomial are 7 and -5.

Question 5.
If the polynomial x⁴ – 6x³ + 16x² – 25x + 10 is divided by another polynomial x² – 2x + k, the remainder comes out to be x + a, find k and a.
Solution:
We have
p(x) = x⁴ – 6x³ + 16x² – 25x + 10
Remainder = x + a   … (i)
Now, we divide the given polynomial 6x³ + 16x² – 25x + 10 by x² – 2x + k.

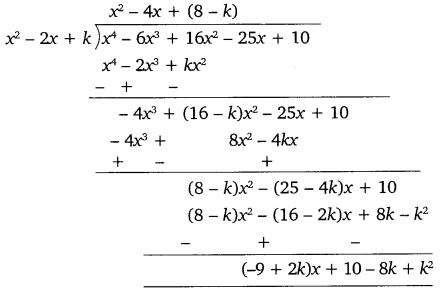
Using equation (i), we get:
(-9 + 2k)x + 10-8 k + k² = x + a
On comparing the like coefficients, we have:
-9 + 2k = 1
⇒ 2k = 10
⇒ k = $\frac { 10 }{ 2 }$ = 5  ….(ii)
and 10 -8k + k²– a   ….(iii)
Substituting the value of k = 5, we get:
10 – 8(5) + (5)² = a
⇒   10 – 40 + 25 = a
⇒  35 – 40 =   a
⇒   a =   -5
Hence, k = 5 and a = -5.