GetStudySolution
Getstudysolution is an online educational platform that allows students to access quality educational services and study materials at no cost.
NCERT Solutions for class 6 Maths chapter 5 – Understanding Elementary Shapes
Back Exercise
Exercise 5.1
Question 1.
What is the disadvantage in comparing line segments by mere observation?
Solution :
Sometimes the difference in lengths betweenthe two line segments is not obvious. So, we are not always sure about our usual judgment.
Question 2.
Why is it better to use a divider than with a ruler, while measuring the length of a line segment?
Solution :
There may be errors due to the thickness of the ruler and angular viewing by using a ruler. These errors are eradicated by using a divider. So, it is better to use a divider, than a ruler, while measuring the length of a line segment.
Question 3.
Draw any line segment, say
Solution :
![]()
Length of AB = 7 cm
Length of BC = 3 cm
Length of AC = 4 cm
AC + CB = 4 cm + 3 cm = 7 cm
But AB = 7 cm
So, AB = AC A- CB.
Question 4.
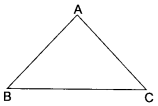
If A, B, C are three points on a line such that AB = 5 cm, BC – 3 cm and AC – 8 cm, which one of them lies between the other two?
![]()
Solution :
AB + BC = AC, so, the point B lies between the point A and point C.
Question 5.
Verify, whether D is the mid-point of AG.
Solution :
AD = AB + BC + CD = 3 units
DG = OE + EF + FG = 3 units
∴ Yes ! D is the mid-point of AG.
![]()
Question 6.
If B is the mid-point of
Solution :
![]()
∴ B is the mid-point of
∴ AB = BC …(1)
∴ C is the mid-point of
∴ BC = CD … (2)
In view of (1) and (2), we get AB = CD.
Question 7.
Draw five triangles and measure their sides. Check in each case, if the sum of the lengths of any two sides is always less than the third side.
Solution :
(i) AB = 3.7 cm
BC = 3 cm
AC = 3.8 cm
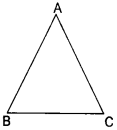
Clearly, AB + BC > AC
BC + AC > AB
AC + AB > BC
(ii) AB = 3 cm
BC = 3 cm
CA = 3 cm
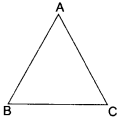
Clearly, AB + BC > AC
BC + AO AB
AC + AB > B C
(iii) AB = 4 cm
BC = 3 cm
AC = 5 cm
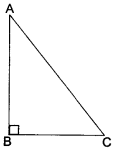
Clearly, AB + BC > AC
BC+ AC > AB
AC + AB > BC.
(iv) AB = 2 cm
BC = 2 cm
AC = 2.8 cm
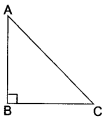
Clearly, AB + BC > AC
BC + AC > AB
AC +AB> BC
(v) AB = 3 cm
BC = 4 cm
CA = 3 cm
Clearly, AB + BC > AC
BC + AC> AB
AC + AB> BC
In each case, we observe that the sum of the lengths of any two sides is always greater than the third side.
Exercise 5.2
Question 1.
What fraction of a clockwise revolution does the hour hand of a clock turn through, when it goes from
(a) 3 to 9
(b) 4 to 7
(c) 7 to 10
(d) 12 to 9
(e) 1 to 10
(f) 6 to 3?
Solution :
(a)
(b)
(c)
(d)
(e)
(f)
Question 2.
Where will the hand of a clock stop, if it
(a) starts at 12 and makes 1/2 of a revolution, clockwise?
(b) starts at 2 and makes 1/2 of a revolution, clockwise?
(c) starts at 5 and makes 1/4 of a revolution, clockwise?
(d) starts at 5 and makes 3/4 of a revolution, clockwise?
Solution :
(a) at 6
(b) at 8
(c) at 8
(d) at 2.
Question 3.
Which direction will you face if you start facing
(a) east and make 1/2 of a revolution clockwise?
(b) east and make 1/2 of a revolution clockwise?
(c) west and make 3/4 of a. revolution anti-clockwise?
(d) south and make one full revolution? (Should we specify clockwise or anti-clockwise for this last question? Why not?)
Solution :
(a) West
(b) West
(c) North
(d) South.
To answer (d), it is immaterial whether we turn clockwise or anti-clockwise because one full revolution will bring us back to the original position.
Question 4.
What part of a revolution have you turned through if you stand to face
(a) east and turn clockwise to face north?
(b) south and turn clockwise to face east?
(c) west and turn clockwise to face east?
Solution :
(a)
(b)
(c)
Question 5.
Find the number of right angles turned through by the hour hand of a clock when it goes from
(a) 3 to 6
(b) 2 to 8
(c) 5 to 11
(d) 10 to 1
(e) 12 to 9
(f) 12 to 9
Solution :
(a) 1 right angle
(b) 2 right angles
(c) 2 right angles
(d) 1 right angle
(e) 3 right angles
(f) 2 right angle
Question 6.
Now many right angles do you make if you start facing
(a) south and turn clockwise to the west?
(b) north and turn anti-clockwise to the east?
(c) west and turn to west?
(d) south and turn to the north?
Solution :
(a) 1 right angle
(b) 3 right angles
(c) 4 right angles
(d) 2 right angles
(clockwise or anticlockwise).
Question 7.
Where will the hour’s hand of a clock stop if it starts
(a) from 6 and turns through 1 right angle?
(b) from 8 and turns through 2 right angles?
(c) from 10 and turns through 3 right angles?
(d) from 7and turns through 2 straight angles?
Solution :
(a) 9
(b) 2
(c) 7
(d) 7.
(We should consider only clockwise direction here).
Exercise 5.3
Question 1.
Match the following :
(i) Straight angle (a) Less than one-fourth a revolution.
(ii) Right angle (b) More than half a revolution
(iii) Acute angle (c) Half of a revolution
(iv) Obtuse angle (d) One-fourth a revolution
(v) Reflex angle (e) Between
Solution :
(i) Straight angle ↔ (c) Half of a revolution
(ii) Right angle ↔ (d) One-fourth a revolution
(iii) Acute angle ↔ (a) Less than one-fourth a revolution
(iv) Obtuse angle ↔ (e) Between 1/4 and 1/2 of a revolution
(v) Reflex angle ↔ (b) More than half a revolution.
Question 2.
Classify each one of the following angles as right, straight, acute, obtuse or reflex :
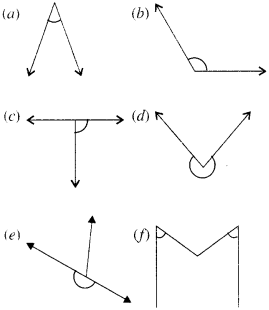
Solution :
(a) Acute
(b) Obtuse
(c) Right
(d) Reflex
(e) Straight
(f) Acute.
Exercise 5.4
Question 1.
What is the measure of
(i) a right angle
(ii) a straight angle?
Solution :
(i) The measure of a right angle is 90°.
(ii) The measure of a straight angle is 180°.
Question 2.
Say True or False:
(a) The measure of an acute angle < 90°.
(b) The measure of an obtuse angle of < 90°.
(c) The measure of reflex angle > 180°.
(d) The measure of one complete revolution = 360°.
(e) If m∠A = 53° and m∠B = 35°, then m∠A > m∠B.
Solution :
(a) True
(b) False
(c) True
(d) True
(e) True.
Question 3.
Write down the measures of
(a) some acute angles.
(b) some obtuse angles. (give at least two examples of each).
Solution :
(a) 23°, 89°
(b) 91°, 179°.
Question 4.
Measure the angles given below, using the Protractor and write down the measure.
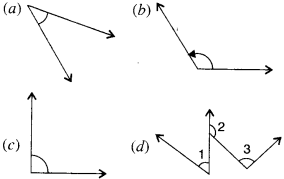
Solution :
(a) 45°
(b) 125°
(e) 90°
(d) ∠l = 40°, ∠2 = 125° and ∠3 = 95°.
Question 5.
Which angle has a large measure? First, estimate and then measure.
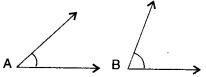
Measure of angle A =
Measure of angle B =
Solution :
Measure of angle A = 40°
Measure of angle B = 65°
The angle B has a larger measure.
Question 6.
From these two angles which have larger measure? Estimate and then confirmed by the measuring them.
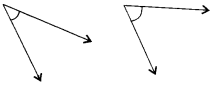
Solution :
Measure of first angle = 45°
Measure of second angle = 60°
The second angle has larger measure.
Question 7.
Fill in the blanks with acute, obtuse, right or straight:
(a) An angle whose measure is less than that of a right angle is. ____________
(b) An angle whose measure is greater than that of a right angle is. ____________
(c) An angle whose measure is the sum of the measures of two right angles is. ____________
(d) When the sum of the measures of two angles is that of a right angle, then each one of them is. ____________
(e) When the sum of the measures of two angles is that of a straight angle and if one of them is acute than the other should be ____________.
Solution :
(a) An angle whose measure is less than that of a right angle is an acute angle.
(b) An angle whose measure is greater than that of a right angle is the obtuse angle (if the angle is less than 180°)
(c) An angle whose measure is the sum of the measures of two right angles is the straight angle.
(d) When the sum of the measures of two angles is that of a right angle, then each one of them is acute.
(e) When the sum of the measures of two angles is that of a straight angle and if one of them is acute than the other should be an obtuse angle.
Question 8.
Find the measure of the angle shown in each figure. (First, estimate with your eye, and then find the actual measurements with a protractor).
(a)
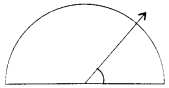
(b)

(c)
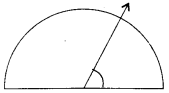
(d)
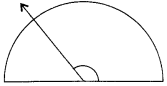
Solution :
Estimation with eye
(a) 45°
(b) 125°
(c) 60°
(d) 135° actual measure with a protractor
Solution :
(a) 40°
(b) 130°
(c) 65°
(d) 135°
Question 9.
Find the angle measure between the hands of the clock in each figure :
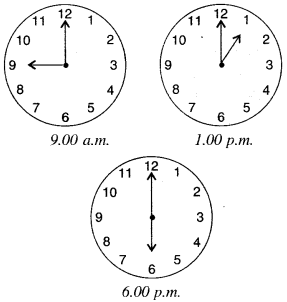
Solution :
- 90°
- 30°
- 180°.
Question 10.
Investigate :
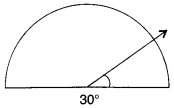
In the given figure, the angle measures 30°. Look at the same figure through a magnifying glass. Does the angle become larger? Does the size of the angle change?
Solution :
No!; No!
Question 11.
Measure and classify each angle :
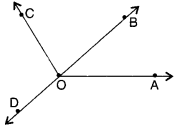
| Angle | Measure | Type |
| ∠AOC | ||
| ∠AOB | ||
| ∠BOC | ||
| ∠DOC | ||
| ∠DOA | ||
| ∠DOB |
Solution :
Angle ∠AOB ∠AOC ∠BOC ∠DOC ∠DOA ∠DOB Measure 40° 120° 80° 105° 140° 180° Type acute obtuse acute obtuse straight.
Exercise 5.5
Question 1.
Which of the following are models for perpendicular lines :
(a) The adjacent edges of a table top.
(b) The lines of a railway track.
(c) The line segments forming the letter “L”.
(d) The letter V.
Solution :
(a) and (c) are models for perpendicular lines.
Question 2.
Let
Solution :
The measure of ∠PAY is 90°.
Question 3.
There are two “set-squares ” in your box. What are the measures of the angles that are formed at their comers? Do they have any angle measure that is common?
Solution :
One is a 30° – 60° – 90° set square; the other is a 45° – 45° – 90° set square. The angle of measure 90° (i.e., a right angle) is common between them.
Question 4.
Study the diagram. The line l is perpendicular to line m.
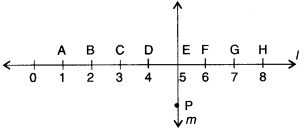
(a) Is CE = EG?
(b) Does PE bisect CG?
(c) Identify any two line segments for which PE is the perpendicular bisector.
(d) Are these true?
(i) AC > EG
(ii) CD = GH
(iii) BC < EH.
Solution :
(a) CE= CD + DE
= 1 + 1=2 units
EG = EF + FG
= 1 + 1=2 units
∴ CE= EG
(b) ∴ CE = EG
∴ E is the mid-point of CG.
∴ Line PE bisects line segment CG
(c) ∴ DE = EF = 1 unit
∴ PE is the perpendicular bisector of line segment DF
∴ BE = EH = 3 units
∴ PE is the perpendicular bisector of BH
(d)
(i) true
(ii) true
(iii) true
Exercise 5.6
Question 1.
Name the types of following triangles:
(a) Triangle with lengths of sides 7 cm, 8 cm and 9 cm.
(b) ΔABC with AB = 8.7cm, AC =7cm andBC = 6 cm.
(c) ΔPQR such that PQ = QR = PR = 5 cm.
(d) ΔDEF with m ∠D = 90°.
(e) ΔXYZ with m ∠Y = 90° and XY = YZ.
(f) ΔLMN with m ∠L = 30°, m ∠M =70° and m ∠N = 80°.
Solution :
(a) Scalene triangle
(b) Scalene triangle
(c) Equilateral triangle
(d) Right angled triangle
(e) Isosceles right triangle
(f) Acute angled triangle.
Question 2.
Match the following :
| Measures of triangle | Type triangle |
| (i) 3 sides of equal length | (a) Scalene |
| (ii) 2 sides of equal length | (b) Isosceles right angled |
| (iii) All sides are of different length | (c) Obtuse angled |
| (iv) 3 acute angles | (d) Right angled |
| (v) 1 right angle | (e) Equilateral |
| (vi) 1 obtuse angle | (f) Acute-angled |
| (vii) 1 right angle with two sides of equal length | (g) Isosceles |
Solution :
| Measures of triangle | Type triangle |
| (i) 3 sides of equal length | (e) Equilateral |
| (ii) 2 sides of equal length | (g) Isosceles |
| (iii) All sides are of different length | (a) Scalene |
| (iv) 3 acute angles | (f) Acute-angled |
| (v) 1 right angle | (d) Right angled |
| (vi) 1 obtuse angle | (c) Obtuse angled |
| (vii) 1 right angle with two sides of equal length | (b) Isosceles right angled |
Question 3.
Name each of the following triangles in two different ways : (you may judge the nature of the angle by observation).
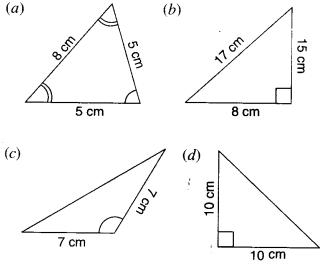
Solution :
(a) Acute-angled and isosceles.
(b) Right-angled and scalene.
(c) Obtuse-angled and isosceles.
(d) Right-angled and isosceles.
(e) Equilateral and acute-angled.
(f) Obtuse-angled and scalene.
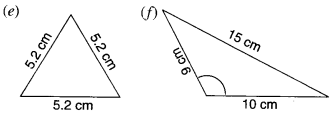
Question 4.
Try to construct triangles using matchsticks. Some are shown here. Can you make a triangle with
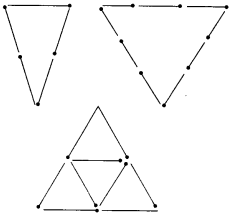
(a) 3 matchsticks?
(b) 4 matchsticks?
(c) 5 matchsticks?
(d) 6 matchsticks?
(Remember you have to use all the available matchsticks in each case). Name the type of triangle in each case. If you cannot make a triangle, think of reasons for it.
Solution :
(a) Yes, an equilateral triangle.
(b) No, since the sum of the lengths of any two sides of a triangle is always greater than the length of the third side.
(c) Yes, an isosceles triangle.
(d) Yes, an equilateral triangle.
Exercise 5.7
Question 1.
Say True or False :
(a) Each angle of a rectangle is a right angle.
(b) The opposite sides of a rectangle are equal in length.
(c) The diagonals of a square are perpendicular to one another.
(d) All the sides of a rhombus are of equal length.
(e) All the sides of a parallelogram are of equal length.
(f) The opposite sides of a trapezium are parallel.
Solution :
(a) True
(b) True
(c) True
(d) True
(e) False
(f) False.
Question 2.
Give reasons for the following :
(a) A square can be thought of as a special rectangle.
(b) A rectangle can be thought of as a special parallelogram.
(c) A square can be thought of as a special rhombus.
(d) Squares, rectangles, parallelograms are all quadrilaterals.
(e) Square is also a parallelogram.
Solution :
(a) A rectangle with all sides equal becomes a square.
(b) A parallelogram with each angle a right angle becomes a rectangle.
(c) A rhombus with each angle a right angle becomes a square.
(d) All these are four-sided polygons made of line segments.
(e) The opposite sides of a square are parallels, so it is a parallelogram.
Question 3.
A figure is said to be regular, if its sides are equal in length and angles are equal in measure. Can you identify the regular quadrilateral?
Solution :
A square is a regular quadrilateral.
Exercise 5.8
Question 1.
Examine whether the following are polygons. If anyone among them is not, say why?
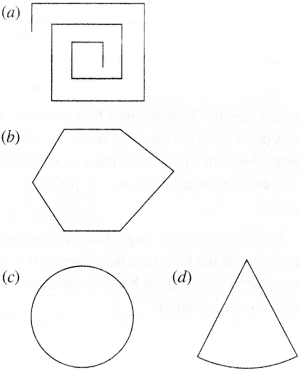
Solution :
(a) is not a closed figure and hence is not a polygon.
(b) is a polygon of six sides.
(c) is not a polygon since it is not made of line segments.
(d) is not a polygon since it is not made of line segments.
Question 2.
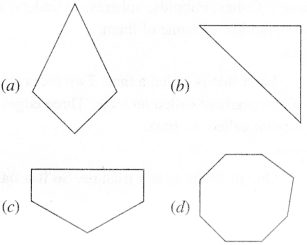
Name each polygon:
Make two more examples of each of these.
Solution :
(a) A Quadrilateral
(b) A Triangle
(c) A Pentagon (5-sided)
(d) An Octagon (8-sided).
Question 3.
Draw a rough sketch of a regular hexagon. Connecting any three of its vertices, draw a triangle. Identify the type of the triangle you have drawn.
Solution :
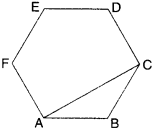
The triangle ABC drawn is an obtuse-angled isosceles triangle.
Question 4.
Draw a rough sketch of a regular octagon. (Use squared paper if you wish). Draw a rectangle by joining exactly four of the vertices of the octagon.
Solution :
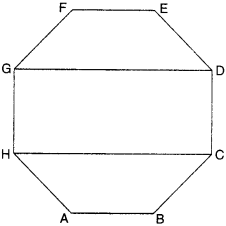
Question 5.
A diagonal is a line segment that joins any two vertices of the polygon and is not a side of the polygon. Draw a rough sketch of a pentagon and draw its diagonals.
Solution :
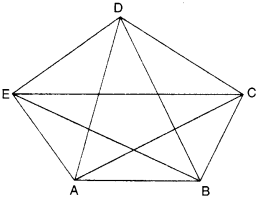
Exercise 5.9
Question 1.
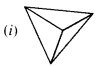
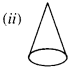
Match the following :
(a) Cone
(b) Sphere
(c) Cylinder
![]()
(d) Cuboid
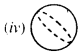
(e) Pyramid
Give two new examples of each shape.
Solution :
(a) ↔ (ii)
(b) ↔ (iv)
(c) ↔ (v)
(d) ↔ (iii)
(e) ↔ (i).
(i) Birthday cap, ice-cream cone
(ii) Tennis Ball, laddu
(iii) Road-roller, gas cylinder
(iv) Brick, book
(v) Pyramids of Egypt, right pyramid.
Question 2.
What shape is
(a) Your installments box?
(b) A brick?
(c) A matchbox?
(d) A road-roller?
(e) A sweet laddu?
Solution :
(a) Cuboid
(b) Cuboid
(c) Cuboid
(d) Cylinder
(e) Sphere.