GetStudySolution
Getstudysolution is an online educational platform that allows students to access quality educational services and study materials at no cost.
NCERT Solutions for class 7 Maths chapter 6 – The Triangle and its Properties
Back Exercise
Exercise 6.1
Question 1.
In ∆PQR, D is the mid-point of
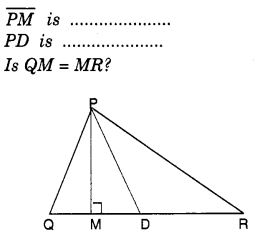
Solution:
PD is the median.
No! QM ≠ MR.
Question 2.
Draw rough sketches for the following:
(a) In ∆ ABC, BE is a median.
(b) In ∆ PQR, PQ and PR are altitudes of the triangle.
(c) In ∆ XYZ, YL is an altitude in the exterior of the triangle.
Solution:

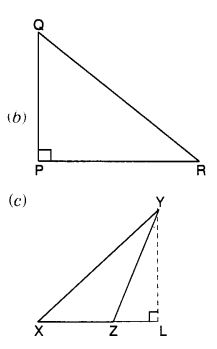
Question 3.
Verify by drawing a diagram if the median and altitude of an isosceles triangle can be the same.
Solution:
AD is the median.
AL is the altitude.
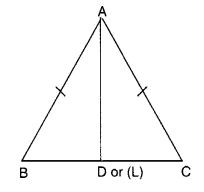
Draw a line segment BC. By paper folding, locate the perpendicular bisector of BC. The folded crease meets BC at D, its mid-point.
Take any point A on this perpendicular bisector. Join AB and AC. The triangle thus obtained is an isosceles ∆ABC in which AB = AC.
Since D is the mid-point of BC, so AD is its median. Also, AD is the perpendicular bisector of BC. So, AD is the altitude of ∆ABC.
Thus, it is verified that the median and altitude of an isosceles triangle are the same.
Exercise 6.2
Question 1.
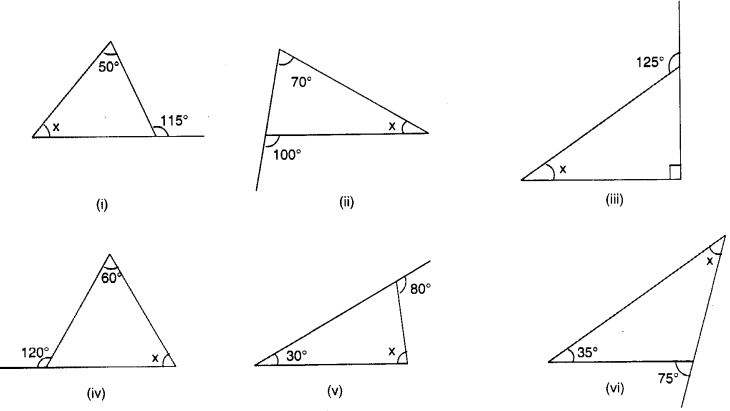
Find the value of the unknown exterior angle x in the following diagrams:
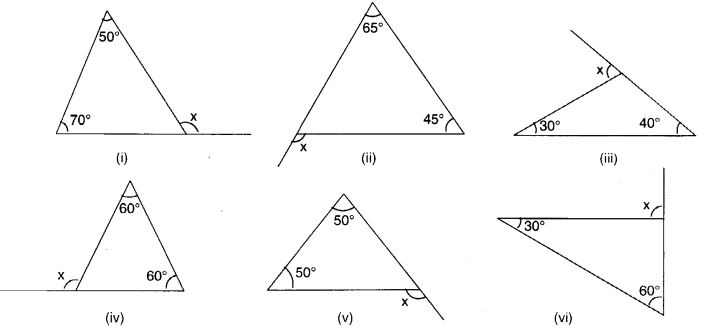
Solution:


Question 2.
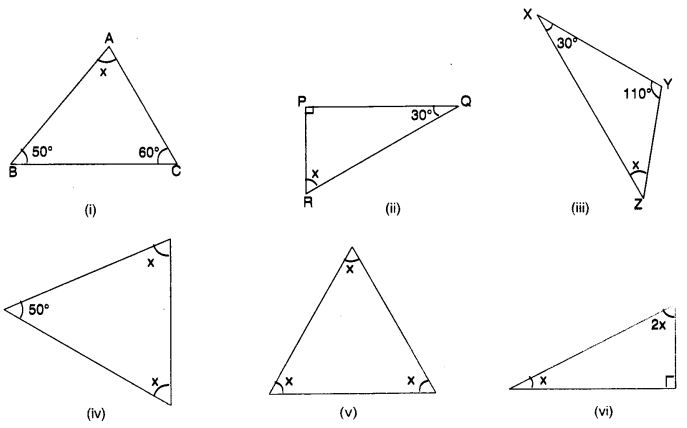
Find the value of the unknown interior angle x in the following figures:
Solution:


Exercise 6.3
Question 1.
Find the value of the unknown x in the following diagrams:
Solution:
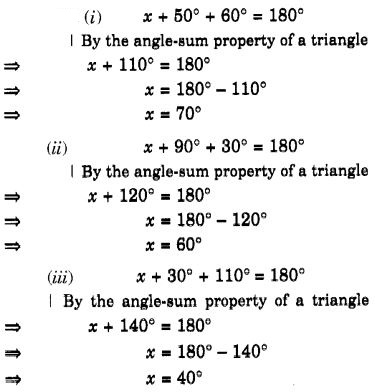

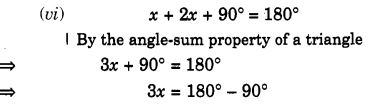

Question 2.
Find the values of the unknowns x and y in the following diagrams:
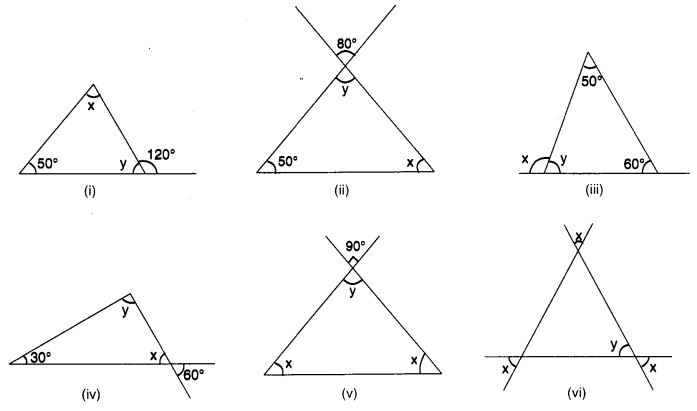
Solution:



Exercise 6.4
Question 1.
Is it possible to have a triangle with the following sides?
- 2 cm, 3 cm, 5 cm
- 3 cm, 6 cm, 7 cm
- 6 cm, 3 cm, 2 cm.
Solution:
- Since, 2 + 3 > 5
So the given side lengths cannot form a triangle. - We have, 3 + 6 > 7, 3 + 7 > 6 and 6 + 7 > 3
i. e., the sum of any two sides is greater than the third side.
So, these side lengths form a triangle. - We have, 6 + 3 > 2, 3 + 2
Undefined control sequence \ngtr 6
So, the given side lengths cannot form a triangle.
Question 2.
Take any point O in the interior of a triangle PQR. Is
- OP + OQ > PQ ?
- OQ + OR > QR?
- OR + OP > RP ?
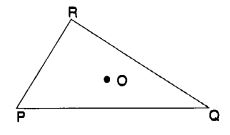
Solution:
- Yes ! OP + OQ > PQ …(1)
Sum of the lengths of any two sides of a triangle is greater than the length of the third side - Yes! OQ + OR > QR …(2)
Sum of the lengths of any two sides of a triangle is greater than the length of the third side - Yes! OR + OP > RP …(3)
Sum of the lengths of any two sides of a triangle is greater than the length of the third side
Question 3.
AM is a median of a triangle ABC. Is AB + BC + CA > 2 AM?
(Consider the sides of triangles ∆ ABM and ∆ AMC.)
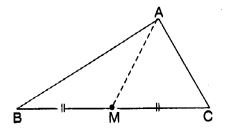
Solution:
Using triangle inequality property in triangles ABM and AMC, we have
AB + BM > AM …(1) and, AC + MC > AM …(2)
Adding (1) and (2) on both sides, we get
AB + (BM + MC) + AC > AM + AM
⇒ AB + BC + AC > 2AM
Question 4.
ABCD is a quadrilateral.
Is AB + BC + CD + DA > AC + BD ?
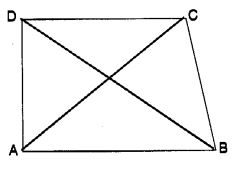
Solution:
In ∆ ABC, AB + BC > AC …(1)
Sum of the lengths of any two sides of a triangle is greater than the length of the third side
In ∆ ACD, CD + DA > AC …(2)
Sum of the lengths of any two sides of a triangle is greater than the length of the third side
Adding (1) and (2),
AB + BC + CD + DA > 2AC …(3)
In ∆ ABD, AB + DA > BD …(4)
Sum of the lengths of any two sides of a triangle is greater than the length of the third side
In ∆ BCD, BC + CD > BD …(5)
Sum of the lengths of any two sides of a triangle is greater than the length of the third side
Adding (4) and (5),
AB + BC + CD + DA > 2BD …(6)
Adding (3) and (6),
2 [AB + BC + CD + DA] > 2 (AC + BD)
⇒ AB + BC + CD + DA > AC + BD.
Question 5.
ABCD is a quadrilateral. Is AB + BC + CD + DA < 2 (AC + BD)?
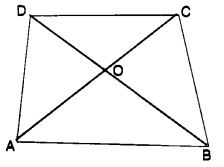
Solution:
In ∆ OAB, OA + OB > AB ….(1)
Sum of the lengths of any two sides of a triangle is greater than the length of the third side.
In ∆ OBC, OB + OC > BC ….(2)
Sum of the lengths of any two sides of a triangle la greater than the length of the third side.
In ∆ OCA,OC + OA > CA ….(3)
Sum of the lengths of any two sides of a triangle is greater than the length of the third side
In ∆ OAD, OA + OD > AD ….(4)
Sum of the lengths of any two sides of a triangle is greater than the length of the third side
Adding (1), (2), (3) and (4),
2(OA + OB + OC + OD) > AB + BC + CD + DA
⇒ AB + BC + CD + DA < 2 (OA + OB + OC + OD)
⇒ AB + BC + CD + DA < 2(OA + OC + OB + OD)
⇒ AB + BC + CD + DA < 2 (AC + BD).
Question 6.
The lengths of the two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall?
Solution:
Let x cm be the length of the third side.
∴ Sum of the lengths of any two sides of a triangle is greater than the length of the third side.
∴ We should have
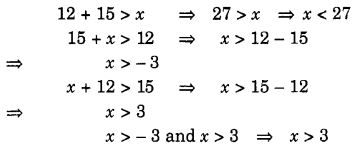
∴ The length of the third side should be any length between 3 cm and 27 cm.
Exercise 6.5
Question 1.
PQR is a triangle right-angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
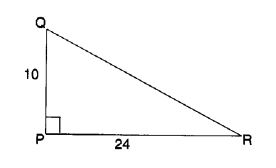
Solution:
QR2 = 102 + 242 By Pythagoras Property
⇒ = 100 + 576 = 676
⇒ QR = 26 cm.
Question 2.
ABC is a triangle right-angled at C. If AB – 25 cm and AC = 7 cm, find BC.
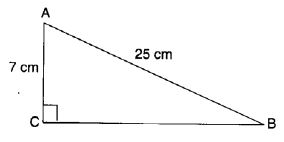
Solution:
AC2 + BC2 = AB2 By Pythagoras Property
⇒ 72 + BC2 = 252
⇒ 49 + BC2 = 625
⇒ BC2 = 625 – 49
⇒ BC2 = 576
⇒ BC = 24 cm.
Question 3.
A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.
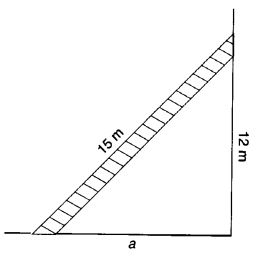
Solution:
Let the distance of the foot of the ladder from the wall be a m. Then,
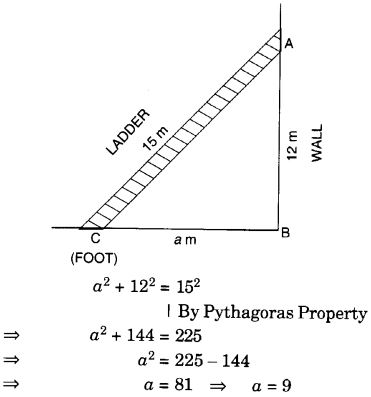
Hence, the distance of the foot of the ladder from the wall is 9 m.
Question 4.
Which of the following can be the sides of a right triangle ?
- 2.5 cm, 6.5 cm, 6 cm.
- 2 cm, 2 cm, 5 cm.
- 1.5 cm, 2 cm, 2.5 cm.
In the case of right-angled triangles, identify the right angles.
Solution:
1. 2.5 cm, 6.5 cm, 6 cm We see that
(2.5)2 + 62 = 6.25 + 36 = 42.25 = (6.5)2
Therefore, the given lengths can be the sides of a right triangle. Also, the angle between the lengths, 2.5 cm and 6 cm is a right angle.
2. 2 cm, 2 cm, 5 cm
∵ 2 + 2 = 4
∴ The given lengths cannot be the sides of a triangle
The sum of the lengths of any two sides of a triangle is greater than the third side
3. 1.5 cm, 2 cm, 2.5 cm We find that
1.52 + 22 = 2.25 + 4 = 6.25 = 2.52
Therefore, the given lengths can be the sides of a right triangle.
Also, the angle between the lengths 1.5 cm and 2 cm is a right angle.
Question 5.
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
Solution:
AC = CD Given
In right angled triangle DBC, DC2 = BC2 + BD2
by Pythagoras Property = 52 + 122 = 25 + 144 = 169
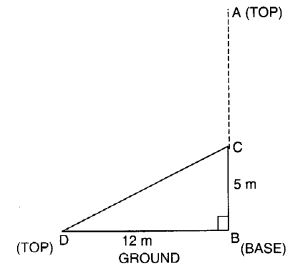
⇒ DC = 13 ⇒ AC = 13
⇒ AB = AC + BC = 13 + 5 = 18
Therefore, the original height of the tree = 18 m.
Question 6.
Angles Q and R of a ∆ PQR are 25° and 65°. Write which of the following is true:
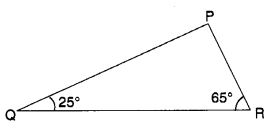
(i) PQ2 + QR2 = RP2
(ii) PQ2 + RP2 = QR2
(iii) RP2 + QR2 = PQ2
Solution:
(ii) PQ2 + RP2 = QR2 is true.
Question 7.
Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.

Solution:
In right-angled triangle DAB, AB2 + AD2 = BD2
⇒ 402 + AD2 = 412 ⇒ AD2 = 412 – 402
⇒ AD2 = 1681 – 1600
⇒ AD2 = 81 ⇒ AD = 9
∴ Perimeter of the rectangle = 2(AB + AD) = 2(40 + 9) = 2(49) = 98 cm
Hence, the perimeter of the rectangle is 98 cm.
Question 8.
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
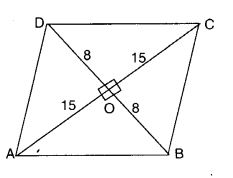
Solution:
Let ABCD be a rhombus whose diagonals BD and AC are of lengths 16 cm and 30 cm respectively.
Let the diagonals BD and AC intersect each other at O.
Since the diagonals of a rhombus bisect each other at right angles. Therefore
BO = OD = 8 cm,
AO = OC = 15 cm,
∠AOB = ∠BOC
= ∠COD = ∠DOA = 90°
In right-angled triangle AOB.
AB2 = OA2 + OB2
By Pythagoras Property
⇒ AB2 = 152 + 82
⇒ AB2 = 225 + 64
⇒ AB2 = 289
⇒ AB = 17cm
Therefore, perimeter of the rhombus ABCD = 4 side = 4 AB = 4 × 17 cm = 68 cm
Hence, the perimeter of the rhombus is 68 cm.