GetStudySolution

Getstudysolution is an online educational platform that allows students to access quality educational services and study materials at no cost.

NCERT Solutions for class 7 Maths chapter 7 – Congruence of Triangles

Back Exercise

Exercise 7.1

Question 1.
Complete the following statements:
(a) Two line segments are congruent if……..
(b) Among two congruent angles, one has a measure of 70°; the measure of the other angle is…….
(c) When we write ∠A = ∠B, we actually mean….
Solution:
(a) they have the same length
(b) 70°
(c) m∠A = m∠B

Question 2.
Give any two real-life examples for congruent shapes.
Solution:

1. Two coins or notes of the same denomination.
2. Two keys of the same lock.

Question 3.
If ∆ ABC = ∆ FED under the correspondence ABC ↔ FED, write all the corresponding congruent parts of the triangles.
Solution:
Corresponding vertices: A and F; B and E; C and D.
Corresponding sides : $\overline { AB }$ and $\overline { FE }$ ; $\overline { BC }$ and $\overline { ED }$; $\overline { CA }$ and $\overline { DF }$.
Corresponding angles: ∠A and ∠F; ∠B and ∠E; ∠C and ∠D.

Question 4.
If ∆ DEF = ∆ BCA, write the part(s) of ∆ BCA that correspond to

1. ∠E
2. $\overline { EF }$
3. ∠F
4. $\overline { DF }$

Solution:

1. ∠C
2. $\overline { CA }$
3. ∠A
4. $\overline { BA }$

Exercise 7.2

Question 1.
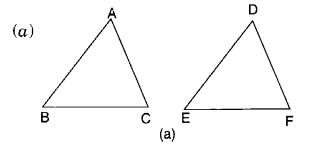
Which congruence criterion do you use in the following?

Given:
So.
AC = DF
AB = DE
BC = EF
so ∆ ABC = ∆ DEF

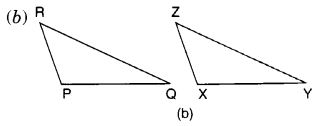
Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ∆ PQR ≅ ∆ XYZ

Given : ∠MLN = ∠ FGH
∠NML = ∠GFH
ML = GF
So, ∆ LMN ≅ ∆ GFH

Given : EB = DB
AE = BC
∠A = ∠C = 90°
So, ∆ ABE ≅ ∆ CDB
Solution:

(a) SSS congruence criterion
(b) SAS congruence criterion
(c) ASA congruence criterion
(d) RHS congruence criterion.

Question 2.
You want to show that ∆ ART ≅ ∆ PEN,

(а) If you have to use SSS criterion, then you need to show
(i)AR = (ii) RT = (iii) AT =

(b) If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
(i) RT = and (ii) PN =

(c) If it is given that AT = PN and you are to use ASA criterion, you need to have
(i) ? (ii) ?
Solution:

Question 3.
You have to show that ∆ AMP = ∆ AMQ.
In the following proof, supply the missing reasons.


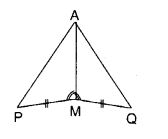
Solution:

Question 4.
In ∆ ABC, ∠A = 30°, ∠B = 40° and ∠C = 110°
In ∆ PQR, ∠P = 30°, ∠Q = 40° and ∠R = 110°
A student says that ∆ ABC = ∆ PQR? by AAA congruence criterion. Is he justified’? Why or why not?
Solution:
No! he is not justified because AAA is not a criterion for congruence of triangles.

Question 5.
In the figure, the two triangles are congruent. The corresponding parts are marked. We can write ∆ RAT = ?

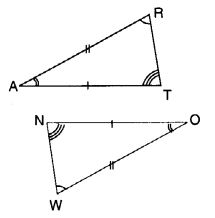
Solution:
∆ RAT ≅ ∆ WON

Question 6.
Complete the congruence statement:


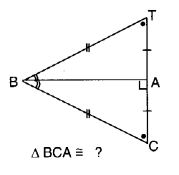
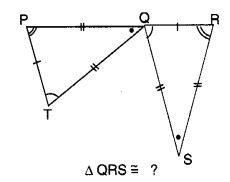
Solution:
∆ BCA = ∆ BTA
∆ QRS = ∆ TPQ

Question 7.
In a squared sheet, draw two triangles of equal areas such that

1. the triangles are congruent
2. the triangles are not congruent. What can you say about their perimeters?

Solution:

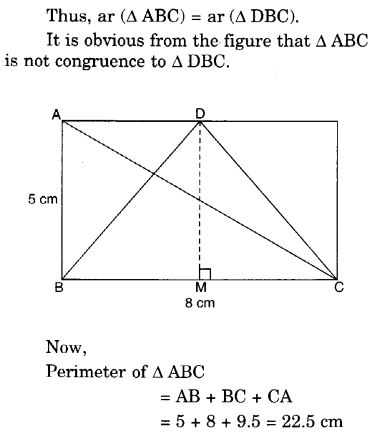
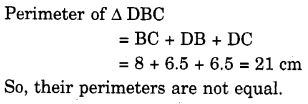
Question 8.
Draw a rough sketch of two triangles such that they have five pairs of congruent parts but still the triangles are not congruent.
Solution:

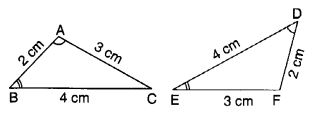
In ∆ ABC and ∆ DEF,
AB = DF (= 2 cm)
BC = ED (= 4 cm)
CA = EF (= 3 cm)
∠BAC = ∠EDF
∠ABC = ∠DEF
But ∆ ABC is not congruent to ∆ DEF.

Question 9.
If ∆ ABC and ∆ PQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?

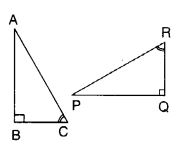
Solution:
BC = RQ by ASA congruence rule.

Question 10.
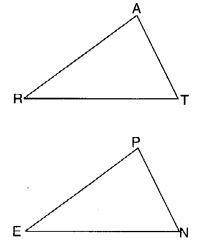
Explain why ∆ ABC ≅ ∆ FED

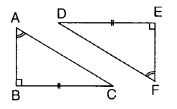
Solution:
∠ABC = ∠FED (= 90°) BC = ED
∠ACB = ∠FDE
∵ The sum of the measures of the three angles of a triangle is 180°.
∆ ABC ≅ ∆ FED (By SAS congruence criterion)