GetStudySolution

Getstudysolution is an online educational platform that allows students to access quality educational services and study materials at no cost.

NCERT Solutions for class 9 Maths chapter 9 – Areas of Parallelograms and Triangles

Back Exercise

Exercise 9.1

Question 1.
Which of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.

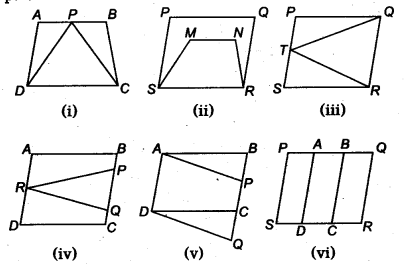
Solution:
In Fig. (i), APDC and trape∠ium ABCD Wes on the same base DC and between the same parallel lines AB and DC.
In Fig. (iii), ATRO and parallelogram PQRS lies on the same base RQ and between the same parallel lies RQ and SP.
In Fig. (v), quadrilateral APCD and quadrilateral ABQD lies on the same base AD and between the same parallel lines AD and BQ.

Exercise 9.2

Question 1.
In figure, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.

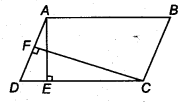
Solution:
We know that,
Area of parallelogram = Base x Altitude
Given, AE = 8 cm CF = 10 cm and AB = 16cm
∴ ar (parallelogramABCD) = DC x AE
= 16 x 8 cm2 (∵ AE = 8 cm)…(i)
and ar (parallelogram ABCD) = AD x CF – AD x 10 ( ∵ CF = 10 cm)
From Eq. (i), we have,
16 x 8 = AD x 10

Question 2.
If E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar (EFGH) = $\frac { 1 }{ 2 }$ ar (ABCD).
Solution:
Given: E,F, G and H are respectively the mid-points of the sides AB, BC, CD and AD. Joint if, it will parallel to CD and AB.
Now, parallelogram HDCF and triangle HGF stand on the same base HF and lie between the same parallel lines DC and HF.

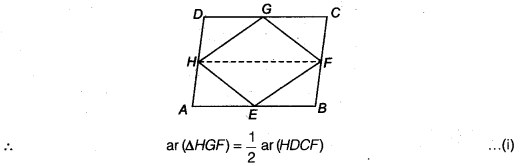
Similarly,parallelogram ABFH and triangle HEF stand on the same base HF and lie between the same parallel lines HF and AB.
ar (∆HEF) = $\frac { 1 }{ 2 }$ ar (∆BFH) …(ii)
On adding Eqs. (i) and (ii), we get
ar (∆HGF) + ar(∆HEF) = $\frac { 1 }{ 2 }$ [ar (HDCF) + ar (ABFH)]
⇒ ar (EFGH) = $\frac { 1 }{ 2 }$ ar (ABCD)

Question 3.
P and Q are any two points lying on the sides DC and AD, respectively of a parallelogram ABCD. Show that ar (APB) = ar(BQC).
Solution:
Given: a parallelogram ABCD. P and Q are any two points lying on the sides DC and AD, respectively.

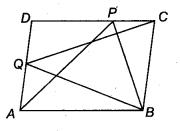
Now, parallelogram ABCD and ABQC stand on the same base BC and lie between the same parallel lines BC and AD.
∴ ar (∆ BQC) = $\frac { 1 }{ 2 }$ ar(ABCD) …(i)
Similarly, ∆ APB and parallelogram ABCD stand on the same base AB and lie between the same parallels AB and CD.
∴ ar (∆ APB) = $\frac { 1 }{ 2 }$ ar (ABCD) ….(ii)
From Eqs. (i) and (ii), we get
ar (∆ APB) = ar (∆ BQC)

Question 4.
In figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar (APB) + ar (PCD) = $\frac { 1 }{ 2 }$ ar (ABCD)
(ii) ar (APD) + ar(PBC) = ar (APB) + ar (PCD)

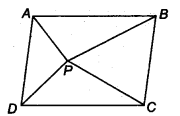
Solution:
Given: ABCD is a parallelogram. So, AB || CD, AD |[ BC.
(i) Now, draw MPR parallel to AB and CD both and also draw a perpendicular PS on AB.
∵ MR || AB and AM || BR

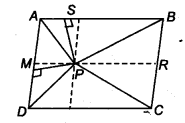
∴ ABRM is a parallelogram so
∴ ar (|| gm ABRM) = AB x PS …(i)
and ar (∆ APB) = $\frac { 1 }{ 2 }$ x AB x PS
ar (∆ APB) = $\frac { 1 }{ 2 }$ ar (|| gm ABRM)
ar (∆PCD) = $\frac { 1 }{ 2 }$ ar (|| gm MRCD)
Now, ar (∆APB) + ar (∆ PCD) = $\frac { 1 }{ 2 }$ ar (|| gm ABRM) + $\frac { 1 }{ 2 }$ ar (||gm MRCD)
= $\frac { 1 }{ 2 }$ ar ( || gm ABCD) …(ii)
(ii) Similarly, we can draw a line through P parallel to AD and through the point P draw perpendicular on AD, we cah prove that
ar (∆APD) + ar (∆PBC) = $\frac { 1 }{ 2 }$ ar (|| gm ABCD) …(iii)
From Eqs. (ii) and (iii), we get
ar (∆APD) + ar (∆PBQ = ar (∆APB) + ar (∆PCD)
Hence proved.

Question 5.
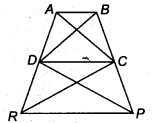
In figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = $\frac { 1 }{ 2 }$ ar (PQRS)

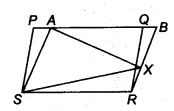
Solution:
Given: PQRS and ABRS both are parallelogram and x is any point on BR.
(i) Here, parallelogram PQRS and ABRS lies on the same base SR and between the same parallel lines SR and PB.
∴ ar (PQRS) = ar (ABRS) …(i)
(ii) Again, in parallelogram ABRS, ∆ AXS and parallelogram lies on the same base AS and between the same parallel lines AS and BR.
∴ ar (∆AXS) = $\frac { 1 }{ 2 }$ar (∆BRS) …(ii)
Now, from Eqs. (i) and (ii), we get
ar (∆AXS) = $\frac { 1 }{ 2 }$ ar (∆ PQRS)

Question 6.
A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In how many parts the fields is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it.
Solution:
Given: PQRS is a parallelogram and A is any point as RS. Now, join PA and PQ. Thus, the field will be divided into three parts and each part is in the shape of a triangle.
Since, the AAPQ and parallelogram PQRS lie on the same base PQ and between same parallel lines PQ and SR.

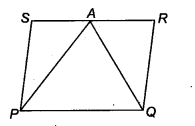
∴ ar (∆APQ) = $\frac { 1 }{ 2 }$ ar (PQRS) ….(i)
Then, remaining
∴ ar (∆ASP) + ar (∆ARQ) = $\frac { 1 }{ 2 }$ ar (PQRS) ….(ii)
Now, from Eqs. (i) and (ii), we get
ar (∆APQ) = ar (∆ASP) + ar (∆ARQ)
So, farmer has two options.
Either the farmer should sow wheat and pulses in ∆APS and ∆AQR or in ar [∆APQ and (∆APS and ∆AQR)] separately.

Exercise 9.3

Question 1.
In figure, E is any point on median AD of a ∆ABC. Show that ar (ABE) = ar (ACE).

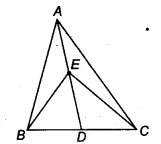
Solution:
Given: AD is a median of AABC and E is a any point on AD.
∵ AD is the median of ∆ABC.
ar (∆ABD) = ar (∆ACD) … (i)
[∵ A median of a triangle divide it into two triangles of equal areas]
Also, ED is the median of ∆EBC.
ar (∆BED) = ar (∆CED) …(ii)
On subtracting Eq. (ii) from Eq. (i), we get
ar (∆ABD) – ar (∆BED) = ar (∆ACD) – ar (∆CED)
⇒ ar (∆ABE) = ar (∆ACE)
Hence proved.

Question 2.
In a triangle ABC, E is the mid-point of median AD. Show that ax (BED) = $\frac { 1 }{ 4 }$ ar (ABC).
Solution:
Given: ABC is a triangle, E is the mid-point of the median AD.

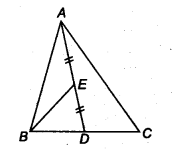
We know that, median divides a triangle into two triangles of equal areas.
∴ ar (∆ABD) = ar (∆ADC)
ar (∆ABD) = $\frac { 1 }{ 2 }$ ar (∆ABC) ……(i)
In ∆ABD, BE is the median.
∴ ar (∆BED) = ar (∆BAE)
or ar (∆BED) = $\frac { 1 }{ 2 }$ ar (∆ABD)
⇒ ar (∆ BED) = 1 x -1 ar (∆ABC) [Put the value from Eq. (i)]
⇒ ar (∆BED) = $\frac { 1 }{ 4 }$ ar (∆ABC)
Hence proved.

Question 3.
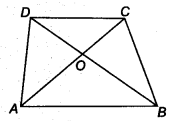
Show that the diagonals of a parallelogram divide it into four triangles of equal area.
Solution:
Given: a parallelogram ABCD. Its diagonals AC and BD intersect at O.

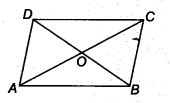
We have to prove that, diagonals AC and BD divides parallelogram into four triangle of equal area i.e.,
ar (∆ OAB) = ar (∆ OBC) = ar (∆ OCD) = ar (∆ OAD)
we know that, the diagonals of a parallelogram bisect each other, so we have OA = OC and OB = OD.
Also, a median of a triangle divides it into two triangles of equal areas.
So, in ∆ABC, BO is the median.
∴ ar (∆OAB) = ar (∆OBC) ,..(i)
Also, in ∆ABD, AO is the median.
∴ ar (∆OAB) = ar (∆OAD) .. ,(ii)
Similarly in AACD, DO is the median.
∴ ar (∆OAD) = ar (∆OCD) .. .(iii)
From Eqs. (i), (ii) and (iii), we get
∴ ar (∆OAB) = ar (∆OBC) = ar (∆OCD) = ar(∆OAD)

Question 4.
In figure, ABC and ABD are two triangles on the same base AB. If line-segment CD is bisected by AB at O, show that
ar(ABC) = ar(ABD)

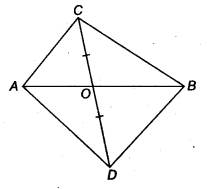
Solution:
Given: ABC and ABD are two triangles on the same base AB.
The line segment CD is bisected by AE = O. ∵ OC = OD
In ∆ACD, we have
OC = OD (Given)
∴ AO is the median.
Since, the median divides a triangle in two triangles of equal areas.
∴ ar (∆AOQ = ar (∆AOD) ….(i)
Similarly, in ∆BCD, ar (BOC) = ar (BOD) …(ii)
On adding Eqs. (i) and (ii), we get
ar (∆ AOC) + ar (∆ BOC) = ar (∆ AOD) + ar (∆ BOD)
⇒ ar (∆ABC) = ar (ABD)

Question 5.
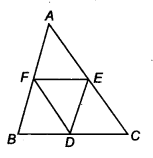
D,E and F are respectively the mid-points of the sides BC, CA and AB of a ∆ABC. Show that
(i) BDEF is a parallelogram.
(ii) ar(∆DEF) = $\frac { 1 }{ 4 }$ ar (∆ABC)
(iii) ar(||gm BDEF) = $\frac { 1 }{ 2 }$ ar(∆ ABC)

Solution:
Given: ABC is a triangle in which the mid-points of sides AB, CA and BC are, respectively F, E, D.

(i) Since, E and F are the mid-points of AC and AB.
∴ BC || EF and EF = $\frac { 1 }{ 2 }$ BC = BD (By mid-point theorem)
Similarly, DE || AB and DE = $\frac { 1 }{ 2 }$ AB = BF
Hence, BDEF is a parallelogram.

(ii) Similarly, we can prove that both FDCE and AFDE are also parallelogram. Now, BDEF is a parallelogram and its diagonal FD divides the parallelogram in two triangles of equal areas.
∴ ar (∆ BDF) = ar (∆ DEF) …(i)
Similarly, in parallelogram ar (∆ EDO) = ar (∆ DEF)
and In parallelogram …(ii)
AFDE, ar (∆ AFE) = ar (∆ DEF) .. .(iii)
From Eqs. (i), (ii) and (iii), we get
ar (∆ AFE) = ar (∆ DEF)
= ar (∆ BDF) = ar (∆ EDC) … (iv)
∵ ar (∆ AFE) + ar (∆ DEF) + ar (∆ EDC) + ar (∆ BDF) = ar (∆ ABC)
∴ 4 [ar (∆ DEF)] = ar (∆ ABC) [From Eq. (iv)]
⇒ ar (∆ DEF) = $\frac { 1 }{ 4 }$ ar (∆ ABC) …(v)

(iii) ar (|| gm BDEF) = ar (∆ DEF) + ar (∆ FBD)
= 2ar (∆ DEF) [From Eq. (iv)]
= 2 . $\frac { 1 }{ 4 }$ ar (∆ ABC) [FromEq. (v)]
= $\frac { 1 }{ 2 }$ ar (A ABC)

Question 6.
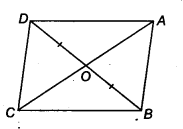
In figure, diagonals AC and BD of quadrilateral ABCD intersect at 0 such that OB = OD. If AB = CD, then show that
(i) ar(DOC) = ar(AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB or ABCD is a parallelogram

Solution:
Given: ABCD is a .quadrilateral and its diagonals AC and BD intersect at O such that OB = OD. Now,
draw DP ⊥ AC and BR ⊥ AC

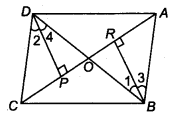
In ∆ DOP and ∆ BOR, we have
∠ DPO = ∠ BRO (Each = 90°)
∠ DOP = ∠BOR (Vertically opposite angles)
and OD = OB (Given)
∴ By AASrule, we get
∆ DOP ≅ ∆ BOR (Each = 90°)
So, ar (∆ DOP) = ar (∆ BOR) ….(i)
Again, in ∆ DCP and ∆ BAR,
∠ DPC = ∠ BRA (Each = 90°)
DC= AB (Given)
and DP = BR ( ∵ ∆ BOR ≅ ∆ DON ⇒ BR = DN)
∴ By SAS rule, we get
∆ DCP = ∆ BAR ….(ii)
∴ ar (∆DCP) = ar (∆ BAR)
On adding Eqs. (i) and (ii), we get
ar (DOP) + ar (DCP) = ar (BOR) + ar (BAP)
Hence, ar (DOC) = ar (AOB)
(ii) ar (DOC) = ar (AOB)
∴ ar (DOC) + ar (BOC) = ar (AOB) + ar (BOC) [Add ar (BOC) on both sides]
⇒ ar (DCB) = ar (ACB)
(iii) Since, ∆ DCS and ∆ACB have equal areas and have the same base. So, ∆ DCB and ∆ ACB must lie between the same parallels.
∴ DA || CB ,
FromEq.(i), ∠1 = ∠4 …(iii)
FromEq. (ii), ∠ 3 = ∠2 …(iv)
On adding Eqs. (iii) and (iv), we get
∠1+∠3 = ∠2 + ∠4
So, ∠ CDB = ∠ ABD
∴ CD|| AB
Hence, ABCD is a parallelogram.

Question 7.
D and E are points on sides AB and AC respectively of ∆ ABC such that ar (DBC) = ar (EBC). Prove that DE || BC.
Solution:
Given, a ∆ ABC and D and E are points on sides AB and AC respectively, also ar (DBQ = ar (ESC)
Therefore, ∆DBC and ∆EBC are equal in area and have a same base BC.
So, altitude from D of ∆DBC = altitude from E of ∆EBC

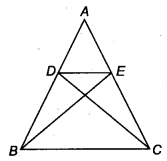
Hence, ∆ DBC and ∆ EBC are between the same parallels.
i.e., DE || BC.

Question 8.
XY is a line parallel to side BC of a ∆ ABC. If BE ||AC and CF || AB meet XY at E and F respectively, show that
ar (ABE) =ar (ACF)
Solution:
Given: a ∆ ABC in which XY || BC also BE || AC is BE || CY and CF || AB i.e., CF || XB.
Now, since XY || SC and CY || BE

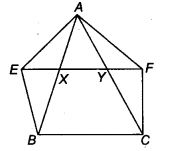
∴ EYCB is a parallelogram.
Since ∆ ABE and parallelogram EYCB lie on the same base BE and between the same parallel lines BE and AC.
So, ar (∆ ABE) = $\frac { 1 }{ 2 }$ ar (EYCB) .. .(i)
Again, CF || AB and XF || BC
∴ BCFX is a parallelogram.
Since, ∆ ACF and parallelogram BCFX lie on the same base CF and between the same parallel lines AB and FC.
∴ ar (∆ ACF) = $\frac { 1 }{ 2 }$ ar (BCFX) …(ii)
Now, parallelogram BCFX and parallelogram BCYE are on the same base BC and between the same parallels BC and EF.
∴ ar (BCFX) = ar (BCYE) …(iii)
From Eqs. (i), (ii) aad (iii), we get
ar (∆ ABE) = ar (∆ ACF)

Question 9.
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then A parallelogram PBQR is completed (see figure).
Show that ax (ABCD) = ar(PBQR).
[Hint Join AC and PQ. Now compare ar (ACQ) and ar (APQ).]

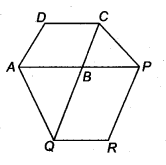
Solution:
Given: two parallelogram ABCD and PBQR.
Join AC and PQ, since PQ and AC and are diagonals of || gm PBQR and || gm ABCD respectively, therefore

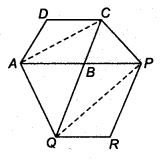
ar (∆ ABC) = $\frac { 1 }{ 2 }$ ar (ABCD) …(i)
[∵ Diagonal of a parallelogram divide it into two triangles of equal area.]
and ar (ABQ) = $\frac { 1 }{ 2 }$ ar (PBQR) .. .(ii)
Now, ∆ACQ and ∆AQP are on the same base AQ and between the same parallels AQ and CP.
∴ ar (ACQ) = ar (AQP)
⇒ ar (ACQ) – ar (ABQ) = ar (AQP) – ar (ABQ) [Subtract ar (ABQ) on both sides]
⇒ ar (∆ ABQ = ar (∆ BPQ)
⇒ $\frac { 1 }{ 2 }$ ar (ABCD) = $\frac { 1 }{ 2 }$ ar (PBQR) [From. Eqs. (i) and (ii)]
⇒ ar (ABCD) = ar (PBQR)

Question 10.
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC)

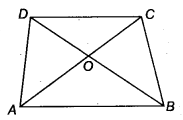
Solution:
Given: diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O.
Now, ∆ ABC and ∆ ABD being on the same base AB and between the same parallels AB and DC.
ar (∆ ABD) = ar (∆ABC)
On subtracting ar (∆AOB) from both sides, we get
ar (∆ ABD) – ar (∆AOB) = ar (∆ABC) – ar (∆AOB)
⇒ ar (∆AOD) = ar (∆BOC)

Question 11.
In figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)
Solution:

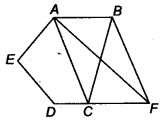
Given, ABCDE is a pentagon and BF || AC.
(i) ∆ACB and ∆ACF being on the same base AC and between the same parallels AC and BF.
∴ ar (∆ ACB) = ar (∆ ACF) …(i)
(ii) ar (AEDF) = ar (AEDQ + ar (∆ACF)
= ar (AEDC) + ar (∆ ACB) [From Eq. (i)]
= ar (ABCDE)

Question 12.
A villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the corners to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
Solution:

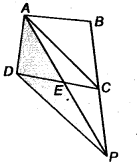
Let ABCD be the plot of land of the shape of a quadrilateral. Let the portion ADE be taken over by the Gram Panchayat of the village from one corner D to construct a Health Centre.
Join, AC draw a line through D parallel to AC to meet BC produced in P. Then, Itwaari must be given the land ECP adjoining his plot so as to from a triangular plot ABP as then.
ar (∆ ADE) = ar (∆ PEC)
Now, ∆ DAP and ∆ DCP are on the same base DP and between the same parallel DP and AC.
∴ ar (∆ DAP) = ar (∆DCP)
⇒ ar (∆ DAP) – ar (∆ DEP) = ar (∆ DCP) – ar (∆ DEP) (Subtracting the same area from both sides)
⇒ ar (∆ ADE) = ar (∆ PCE)
⇒ ar (∆ DAE) + ar (ABCD) = ar (∆PCE) + ar (ABCE) (Adding the same area on both sides)
⇒ ar (ABCD) = ar (∆ABP)

Question 13.
ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ADX) = ar(ACY). [Hint Join IX]
Solution:
Given: ABCD is a trapezium and AB || CD. Also, XY || AC.
Now, join CX. Since, ∆ ADX and ∆ACX lie on the same base AX and between the same parallel lines AB and DC.

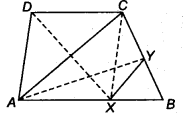
∴ ar(∆ ADX) = ar(∆ ACX) …(i)
Again, ∆ ACX and ∆ ACY lie on the same base AC and between the same parallel lines AC and XY.
∴ ar(∆ ACX) = ar(∆ ACY) …(ii)
Hence, from Eqs. (i) and (ii), we get
ar(∆ ADX) = ar(∆ ACY)

Question 14.
In figure, AP || BQ || CR. Prove that ar(AQC) = ax(PBR).

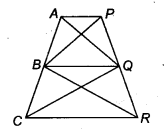
Solution:
According to given figure, we get
ar (∆PBR) = ar (∆PBQ) + ar (∆QBR) …..(i)
and ar(∆ AQC) = ar (∆ AQB)+ ar (∆ BQC) …(ii)
Since, ar(∆ BQC) = ar (∆ QBR) …(iii)
[Since, ∆BQC and ∆QBR lie on the same base BQ and between the same parallel lines BQ and CR]
Similarly, ar (AQB) = ar (PBQ) …..(iv)
On adding Eq. (iii) and (iv), we get
ar (∆BQC + ar(∆AQB) = ar (∆QBR) + ar (∆PBQ).
On putting the values from Eqs. (i) and (ii), we get
ar(∆ AQC) = ar(∆ PBR)

Question 15.
Diagonals AC and BD of a quadrilateral ABCD intersect at 0 in such a way that ax(AOD) = ar(BOC). Prove that ABCD is a trapezium.
Solution:
Given: ABCD is a quadrilateral and diagonal AC and BD intersect at O. Also,

ar(∆ AOD) = ar(∆ BOC)
On adding both sides ar (∆ AOB), we get
ar(∆ AOD) + ar(∆ AOB) = ar(∆ BOC) + ar(∆ AOB)
⇒ ar(∆ ADB) = ar(∆ ACB)
Now, ∆ ACB and ∆ ADB lie on same base AB
and ar(∆ ADB) = ar(∆ ACB)
Hence, ∆ ACB and ∆ ADB lie between same parallel lines.
∴ AB || DC
Hence, ABCD is a trapezium.

Question 16.
In figure ax(DRC) = ar(DPC) and ai(BDP) = ar(ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.

Solution:
Given,
ar (∆ DPC) = ar(∆ DRC) ……(i)
and ar(∆ BDP) = ar(∆ ARC) ……(ii)
On subtracting Eq. (i) from Eq. (ii), we get
ar(∆ BDP) – ar(∆ DPC) = ar(∆ ARC) – ar(∆ DRC)
⇒ ar(∆ BDC) = ar(∆ ADC)
Since, these two triangles are on the same base DC.
∴ DC || AB
Hence, ABCD is a trapezium.
Also, ar(∆ DRQ = ar(∆ DPQ
Since both triangles have the same base DC.
∴ RP || DC
Hence, PRCD is a trapezium.

Exercise 9.4

Question 1.
Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
Solution:
Given: parallelogram ABCD and rectangle ABEF are on same base AB, and area of both are equal.
In rectangle ABEF, AB = EF and in parallelogram ABCD,
CD = AB ⇒ AB + CD = AB + EF ….(i)
We know that, the perpendicular distance between two parallel sides of a parallelogram is always less than the length of the other parallel sides.

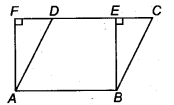
∴ BE < SC and AF < AD On adding both, we get, BC + AD > BE + AF …(ii)
⇒ BC + AD + AB + CD > BE + AF + AB + CD (Adding AB + CD on both sides)

⇒ AB + BC+ CD + AD > AB + BE + EF + AF [Put the values from Eq. (i)]
Hence, the perimeter of the parallelogram is greater than the perimeter of the rectangle.

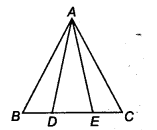
Question 2.
In figure, D and E are two points on BC such that BD = DE = EC. Show that ar(ABD) = ar(ADE) = ar(AEC). Can you now answer the question that you have left in the Introduction’ of this chapter, whether the field of Budhia has been actually divided into three pares of equal area?
[Remark Note that by taking BD = DE = EC, the ∆ ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the sameway, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide ∆ ABC into n triangles of equal areas.]
Solution:
Given: ABC is a triangle and D and E are two points on BC, such that

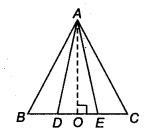
BD = DE = EC
Let AO be the perpendicular to BC.
∴ ar ( ∆ABD) = $\frac { 1 }{ 2 }$ x BD x AO
ar (∆ADE) = $\frac { 1 }{ 2 }$ x DE x AO
and ar(∆AEC) = $\frac { 1 }{ 2 }$ x EC x AO
Since, BD = DE = EC (Given)
∴ ar(∆ABD) = ar(∆ADE) = ar(∆AEC)
Yes, altitudes of all triangles are same. Budhia has use the result of this question in dividing her land in three equal parts.

Question 3.
In figure, ABCD, DCFE and ABFE are parallelograms. Show that ar(ADE) = ax(BCF).

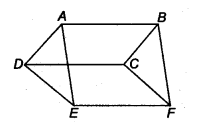
Solution:
Given: ABCD, DCFE, and ABFE and parallelograms
In ∆ADE and ∆BCF,
AD = BC (∵ ABCD is a parallelogram)
DE – CF (∵ DCFE is a parallelogram)
and AE = BF (∵ ABFE is a parallelogram)
Hence ∆ADE = ∆BCF
∴ ar (∆ADE) = ar (∆BCF)

Question 4.
In figure, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar(BPC) = ax(DPQ).[Hint Join AC.]

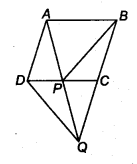
Solution:
Given: ABCD is a parallelogram and AD || CQ, and AQ = CQ. Join the line segment AC.
Now, ∆ APC and ∆ BPC lie on the same base PC and between the same parallels PC and AB, therefore
ar(∆ APC) = ar(∆ BPC) …(i)
AD = CQ and AD || CQ (Given)

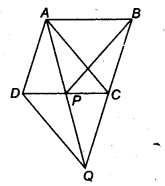
Thus, in quadrilateral ACQD, one pair of opposite sides is equal and parallel.
∴ ADQC is a parallelogram.
We know that, diagonals of a parallelogram bisect each other.
∴ CP = DP and AP = PQ ….(ii)
In ∆ APC and ∆ DPQ, we have

Question 5.
In figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, Show that

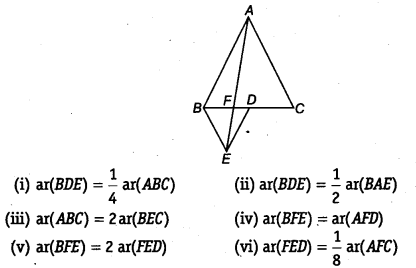
[Hint Join EC and AD. Show that BE || AC and DE || AB, etc.]
Solution:
Join AD and EC. Let x be the side of ∆ ABC. Then
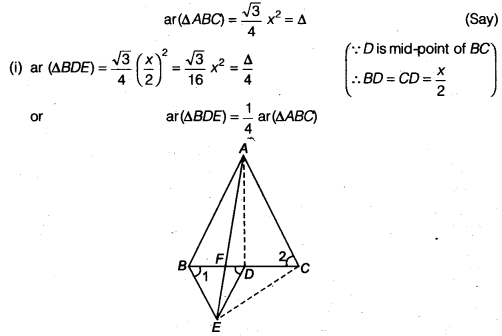img src=”https://farm2.staticflickr.com/1921/31706925298_d4d194aabd_o.png” width=”525″ height=”586″ alt=”NCERT Solutions for Class 9 Maths Chapter 10 Areas of Parallelograms and Triangles 10.4 5b”>

Question 6.
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that
ar(APB) x ar(CPD) = ar(APD) x ar(BPC).
[Hint From A and C, draw perpendiculars to BD.]
Solution:
Given: ABCD is a quadrilateral whose diagonals intersect at P.
Draw two perpendiculars AE and CF from A and Con BD, respectively. Now,
LHS = ar (∆ APB) x ar (∆ CPD)


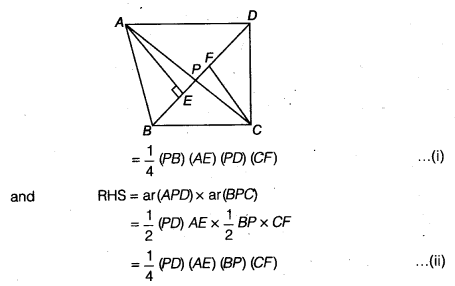
From Eqs. (i) and (ii), we get, LHS = RHS
i.e., ar(∆APB) x ar(∆CPD) = ar(∆APD) x ar(∆BPC)

Question 7.
P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that

Solution:
(i) Given: P and Q are mid-points of AB and BC. Also, R is mid-point of AP.
Since, P and 0 are the mid-points of AB and BC, respectively.
∴ PQ || AC and PQ = $\frac { 1 }{ 2 }$ AC (By mid-point theorem)
Draw RM || AC || PQ
Also, draw QG ⊥ RM and MH ⊥ AC
∵ PQ || RM || AC and PR = RA
∴ QM = MC
In ∆ QGM and ∆ MHC,

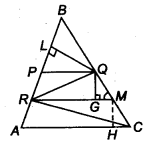
Question 8.
In figure, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that

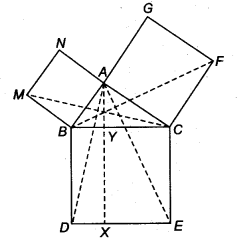
(i) ∆MBC = ∆ABD
(ii) ar(BYXD) = 2 ar(MBC)
(iii) ar(BYXD) = ax(ABMN)
(iv) ∆FCB ≅ ∆ACE
(v) ar(CYXE) = 2 ar(FCB)
(vi) ar(CYXE) = ax(ACFG)
(vii) ar(BCED) = ar(ABMN) + ar(ACFG)
Note: Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler, proof of this theorem in Class X.
Solution:
(i) In ∆ABD and ∆MBC,
BC = BD (These are the sides of square)
MB = AB
and ∠ MBC = 90° + ∠ ABC
= ∠DBC + ∠ABC
= ∠ABD
∴ ∆MBC = ∆ABD (By SAS rule)

(ii) From part (i), ar(∆ MBC) = ar (∆ ABD) …(i)
But ar(∆ ABD) = $\frac { 1 }{ 2 }$ ar (BYXD) …(ii)
(∵ ∆ ABD and rectangle BYXD lie on the same base and between same parallel between lines.)
From Eqs. (i) and (ii), we get
ar (∆MBC) = $\frac { 1 }{ 2 }$ ar (BYXD) .. .(iii)
⇒ ar (BYXD) = 2 ar (∆MBC)

(iii) Now ar (∆MBC) = $\frac { 1 }{ 2 }$ ar (ABMN) …..(iv)
(∵ ∆MBC and square ABMN lie on the same base MB and between same parallels MB and NC)
From Eqs. (iii) and (iv), we get
ar (BYXD) = ar (ABMN)

(iv) In ∆ ACE and ∆FCS,
AC = FC
and CE = BC (These are the sides of square)
∠ FCB = 90° + ∠ ACB = ∠ BCE + ∠ACB = ∠ACE
So, ∆ FCB = ∆ ACE (By SAS rule)

(v) From Eqs. (iv), ar(AACE) = ar(AFCB) …(vi)
But ar(∆ACE) = $\frac { 1 }{ 2 }$ ar(CVXE)
(∵ Both lie on the same base CE and between same parallel lines CE and AX.)
From Eqs. (vi) and (vii), we get
ar (∆ACE) = $\frac { 1 }{ 2 }$ ar (CYXE)
= ar (∆FCB) …(vii)
⇒ ar (CYXE) = $\frac { 1 }{ 2 }$ ar (∆ FCB)

(vi) Now, ar(AFCB) = $\frac { 1 }{ 2 }$ ar (ACFG) …(ix)
(∵Both lie on same base CF and between same parallel lines CF and BG)
From Eqs. (viii) and (ix), we get
$\frac { 1 }{ 2 }$ ar (ALFG) = $\frac { 1 }{ 2 }$ ar (CYXE)
⇒ ar (ACFG) = ar (CYXE)

(vii) Now, ar (BCED) = ar (BYXD) + ar (CYXE)
= ar (ABMN) + ar (ACFG) [From part (iii) and (vi)]