GetStudySolution
Getstudysolution is an online educational platform that allows students to access quality educational services and study materials at no cost.
NCERT Solutions for class 5 Maths chapter 9 – Boxes and Sketches
Back Exercise
Page No 127:
Question 1:
Buddha wants to make a paper cube using a squared sheet. He knows that all the faces of a cube are squares. He draws two different shapes.
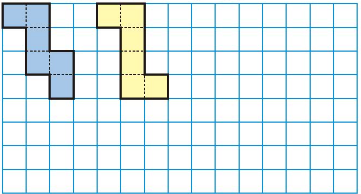
• Will both these shapes fold into a cube? • Draw at least one more shape which can fold into a cube. • What will be the area of each face of the cube? • Draw one shape which will not fold into a cube. • Look around and discuss which things around you look like a cube. List a few.
Answer:
• Yes, both the shapes will fold into a cube.
• The shape which can fold into a cube is shown below. .png)
• We know that, each face of the cube is a small square. Area of small square is 1 square cm. Thus, the area of each face of the cube is 1 square cm.
• The shape which cannot fold into a cube is shown below. (1).png)
• The shape of die, sugar cubes, ice cubes, etc. resembles that of a cube.
Page No 128:
Question 1:
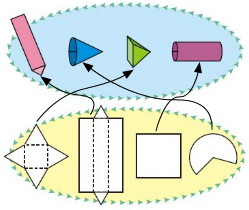
All boxes are not cubes. Here are some different kinds of boxes. Match each shape below with a box into which it will fold.
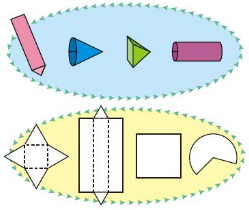
Answer:
Page No 129:
Question 1:
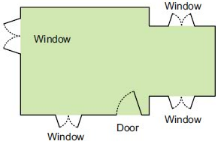For making a house a floor map is first made. Have you ever seen a floor map? Here is a floor map of Vibha’s house. It shows where the windows and the doors are in the house.
• Which is the front side of her house? How many windows are there on the front side?
(a) .png)
(b) .png)
(c) .png)
(d) .png)
Here are four deep drawings of houses.
• Which one is Vibha’s house?
• Why do the other three deep drawings not match the floor map? Discuss.
Answer:
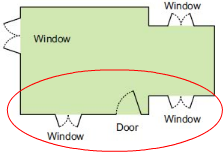
• Front side of Vibha’s house is encircled in the above image.There are two windows and one door on the front side of the house.
• The front side of Vibha’s house has one door and two windows.
• The figure (c) represents Vibha’s house.
Page No 130:
Question 1:
Look at this floor map of a house. Make doors and windows on the deep drawing of this house.
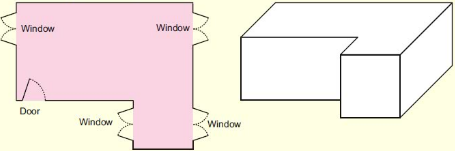
• Are there any windows you couldn’t show on the deep drawing? Circle them on the floor map.
Answer:
The doors and windows on the deep drawing of the house is shown below.
.png)
There are 2 windows that could not be shown on the deep drawing. These windows are encircled on the floor map as shown below.
.png)
Question 2:
Soumitro and his friends made deep drawings of a cube.
These are their drawings.
(a) .png)
(b) .png)
(c) .png)
(d) .png)
(e) .png)
(f) .png)
(g) .png)
• Which of the drawings look correct to you? Discuss. • Can you add some lines to make drawing (f) into a deep drawing of the cube?
Answer:
• The drawings (d), (e) and (g) are correct.
• The deep drawing of a cube after adding lines to figure (f) is shown below:
(2).png)
Page No 131:
Question 1:
This cut-out is folded to make a cube.
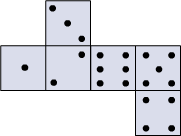
Which of these are the correct deep drawings of that cube? (a)
.png)
(b)
.png)
(c)
.png)
(d)
.png)
(e) .png)
Answer:
The correct deep drawings of the given cube are :
Question 2:
Make a deep drawing of a box which looks like this.
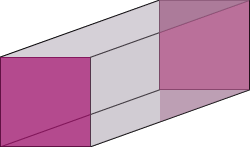
Answer:
The deep drawing of the given box is shown below.
.png)
Page No 133:
Question 1:
• If you look at the bridge from the top, how will it look? Choose the right drawing below:
a) .png)
b) .png)
• Look at the photo and try to make a deep drawing of this bridge.
Answer:
The top view of the bridge is shown below.
The deep drawing of the bridge is shown below.
.png)
Question 2:
Make drawings to show how this bridge will look • From the top • From the front • From the side
Answer:
The top view of the bridge is shown below.
.png)
The front view of the bridge is shown below.
(1).png)
The side view of the bridge is shown below.
 (1).png)
Question 3:
Make a matchbox model which looks like this.
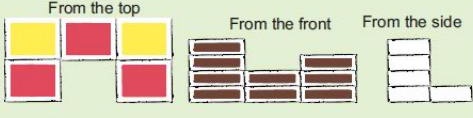• Also make a deep drawing of the model in your notebook.
Answer:
Disclaimer: Students are advised to prepare the answer on their own.
Question 4:
How many cubes are needed to make this interesting model?
• Here are some drawings of the model. Mark the correct top view drawing with ‘T’ and the correct side view drawing with ‘S’. .png)
(a) .png)
(b) .png)
(c) (3).png)
(d)
.png)
Answer:
Number of cubes in the top layer = 4 + 5 = 9 Number of cubes in the second layer from top = 4 + 5 + 3 + 4 = 16 Number of cubes in the third layer from top = 4 + 5 + 3 + 4 + 2 + 3 = 21 Number of cubes in the fourth layer from top = 4 + 5 + 3 + 4 + 2 + 3 + 2 + 1 = 24 Number of cubes in the bottom layer = 4 + 5 + 3 + 4 + 2 + 3 + 2 + 1 + 1 = 25
Total number of cubes in the model = 9 + 16 + 21 + 24 + 25 = 95
The correct drawing for the top and side view is given below:
T , S